Упражнение 981 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№981 учебника 2023-2025 (стр. 220):
Решите систему неравенств:
а) \(\begin{cases} 57 - 7x > 3x - 2, \\ 22x - 1 < 2x + 47; \end{cases}\)
б) \(\begin{cases} 1 - 12y < 3y + 1, \\ 2 - 6y > 4 + 4y; \end{cases}\)
в) \(\begin{cases} 102 - 73z > 2z + 2, \\ 81 + 11z \geq 1 + z; \end{cases}\)
г) \(\begin{cases} 6 + 6,2x \geq 12 - 1,8x, \\ 2 - x \geq 3,5 - 2x. \end{cases}\)
№981 учебника 2013-2022 (стр. 217):
Преобразуйте в дробь выражение:
а) \((a^{-1} + b^{-1})(a + b)^{-1}\);
б) \((a - b)^{-2}(a^{-2} - b^{-2})\).
Подсказка
№981 учебника 2023-2025 (стр. 220):
Вспомните:
- Решение систем неравенств с одной переменной.
- Числовые промежутки.
- Решение неравенств с одной переменной.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
- Десятичная запись дробных чисел.
- Деление десятичных дробей.
- Деление рациональных чисел.
- Сложение и вычитание десятичных дробей.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
№981 учебника 2013-2022 (стр. 217):
Вспомните:
- Степень с целым отрицательным показателем.
- Степень с натуральным показателем.
- Обыкновенные дроби.
- Взаимно обратные дроби.
- Сложение и вычитание рациональных дробей с разными знаменателями.
- Основное свойство рациональной дроби.
- Умножение рациональных дробей.
Ответ
№981 учебника 2023-2025 (стр. 220):
а) \(\begin{cases} 57 - 7x > 3x - 2, \\ 22x - 1 < 2x + 47 \end{cases}\)
\(\begin{cases} -7x - 3x > -2 - 57, \\ 22x - 2x < 47+1 \end{cases}\)
\(\begin{cases} -10x > -59, / : (-10) \\ 20x < 48 / : 20 \end{cases}\)
\(\begin{cases} x < \frac{59}{10}, \\ x < \frac{48}{20} \end{cases}\)
\(\begin{cases} x < 5,9, \\ x < 2,4 \end{cases}\)
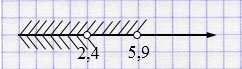
Ответ: \((- \infty; 2,4)\).
б) \(\begin{cases} 1 - 12y < 3y + 1, \\ 2 - 6y > 4 + 4y \end{cases}\)
\(\begin{cases} -12y - 3y < 1 - 1, \\ -6y - 4y > 4 - 2 \end{cases}\)
\(\begin{cases} -15y < 0, / : (-15) \\ -10y > 2 / : (-10) \end{cases}\)
\(\begin{cases} y > 0, \\ y < -0,2 \end{cases}\)
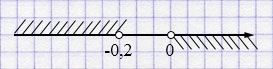
Ответ: нет решения.
в) \(\begin{cases} 102 - 73z > 2z + 2, \\ 81 + 11z \geq 1 + z \end{cases}\)
\(\begin{cases} -73z - 2z > 2 - 102, \\ 11z - z \geq 1 - 81 \end{cases}\)
\(\begin{cases} -75z > -100, / : (-75) \\ 10z \geq -80 / : 10 \end{cases}\)
\(\begin{cases} -75z > -100, / : (-75) \\ 10z \geq -80 / : 10 \end{cases}\)
\(\begin{cases} z < \frac{100}{75}, \\ z \geq -8 \end{cases}\)
\(\begin{cases} z < \frac{4}{3}, \\ z \geq -8 \end{cases}\)
\(\begin{cases} z < 1\frac{1}{3}, \\ z \geq -8 \end{cases}\)
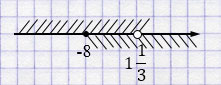
Ответ: \([-8; 1\frac{1}{3})\).
г) \(\begin{cases} 6 + 6,2x \geq 12 - 1,8x, \\ 2 - x \geq 3,5 - 2x \end{cases}\)
\(\begin{cases} 6,2x +1,8x \geq 12 - 6, \\ -x + 2x \geq 3,5 - 2 \end{cases}\)
\(\begin{cases} 8x \geq 6, / : 8 \\ x \geq 1,5 \end{cases}\)
\(\begin{cases} x \geq \frac68, \\ x \geq 1,5 \end{cases}\)
\(\begin{cases} x \geq \frac34, \\ x \geq 1,5 \end{cases}\)
\(\begin{cases} x \geq 0,75, \\ x \geq 1,5 \end{cases}\)
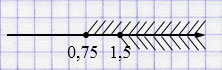
Пояснения:
Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.
При решении неравенств системы используем то, что:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Если знак неравенства строгий (\(>\) или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.
Если знак неравенства нестрогий (\(\geq\) или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.
У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.
№981 учебника 2013-2022 (стр. 217):
а) \((a^{-1} + b^{-1})(a + b)^{-1} =\)
\(=\left(\dfrac{1}{a} + \dfrac{1}{b}\right) \cdot \dfrac{1}{a + b}=\)
\(= \dfrac{\cancel{a + b}}{ab} \cdot \dfrac{1}{\cancel{a + b}} = \dfrac{1}{ab}\)
б) \((a - b)^{-2}(a^{-2} - b^{-2}) =\)
\(=\dfrac{1}{(a - b)^2} \cdot \left(\dfrac{1}{a^2} - \dfrac{1}{b^2}\right)=\)
\(= \dfrac{1}{(a - b)^2} \cdot \dfrac{b^2 - a^2}{a^2b^2} = \)
\(=\dfrac{-(a^2 - b^2)}{a^2b^2(a - b)^2}=\)
\(= -\dfrac{\cancel{(a - b)}(a + b)}{a^2b^2(a - b)^{\cancel{2}}} = \)
\(=-\dfrac{a + b}{a^2b^2(a - b)}\).
Пояснения:
Основные правила отрицательных степеней:
\[ a^{-n} = \frac{1}{a^n}, \quad \frac{1}{a^{-n}} = a^n. \]
1. Все отрицательные показатели заменяем дробями с положительными степенями.
2. В пункте (а) выражение \((a^{-1} + b^{-1})\) приводим к общему знаменателю \(ab\), получаем \(\dfrac{a+b}{ab}\).
3. Умножаем на \((a + b)^{-1} = \dfrac{1}{a+b}\), что даёт \(\dfrac{1}{ab}\).
4. В пункте (б) раскрываем разность дробей \(\dfrac{1}{a^2} - \dfrac{1}{b^2}\), получаем разность квадратов числителей и сокращаем общий множитель \((a - b)\).
Итоговое выражение содержит только положительные показатели степеней и записано в виде простой дроби.
Вернуться к содержанию учебника