Упражнение 860 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(a < b\), \(c > b\), \(c < d\), \(a > e\)

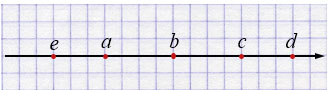
Пояснения:

Чтобы правильно расположить точки на координатной прямой, нужно учесть все данные неравенства.

Даны условия:

1) \(a < b\) — значит, \(a\) левее \(b\);

2) \(c > b\) — значит, \(c\) правее \(b\);

3) \(c < d\) — значит, \(c\) левее \(d\);

4) \(a > e\) — значит, \(a\) правее \(e\).

Итоговый порядок точек на прямой:

\[ e < a < b < c < d. \]

а) \(\dfrac{\sqrt{7-14x}}{x+8}\)

1) \(7 - 14x \geqslant 0\)

\(-14x \geqslant -7\)   \(/ : (-14)\)

\(x \leqslant \dfrac{7}{14}\)

\(x \leqslant \dfrac{1}{2}\)

\(x \leqslant 0,5\)

2) \(x+8 \neq 0\)

\(x \neq -8\).

Ответ: \(x \in (-\infty; -8)\cup (-8; 0,5]\).

б) \(\dfrac{6}{\sqrt{4-x}-1}\)

1) \(4 - x \geqslant 0\)

\(x\leqslant 4\)

2) \(\sqrt{4-x}-1 \neq 0\)

\(\sqrt{4-x} \neq 1\)

\(4 - x \neq 1\)

\(-x \neq 1 - 4\)

\(-x\neq-3\)

\(x \neq3\)

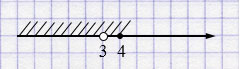
Ответ: \(x \in (-\infty; 3)\cup (3; 4]\).

Пояснения:

При нахождении области определения функций, нужно учитывать то, что:

— подкоренное выражение должно быть неотрицательным (\(\geqslant 0\));

— знаменатель должен быть отличен от нуля.

Составляем неравенства относительно подкоренных выражений. При решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

Точку, в которой знаменатель не равен нулю, на координатной прямой делаем "выколотой" (незакрашенной), так как в этой точке функция не существует и, записывая промежутки, около этой точки ставим круглую скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.