Упражнение 846 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(\frac{a}{b}\), где \(a\) и \(b\) — натуральные числа

1) \(a < b\)

Пусть \(a = 2\), \(b = 3\), то \(\frac{a}{b} = \frac23\)

\(\frac{a+1}{b+1} = \frac{2 + 1}{3 + 1} = \frac34\)

\(\frac23 ^{\color{blue}{\backslash4}} < \frac34 ^{\color{blue}{\backslash3}} \)

\(\frac{8}{12} < \frac{9}{12} \) - дробь увеличится.

2) \(a > b\)

Пусть \(a = 3\), \(b = 2\), то \(\frac{a}{b} = \frac32\)

\(\frac{a+1}{b+1} = \frac{3 + 1}{2 + 1} = \frac43\)

\(\frac32 ^{\color{blue}{\backslash3}} < \frac43 ^{\color{blue}{\backslash2}} \)

\(\frac{9}{6} > \frac{8}{6} \) - дробь уменьшится.

3) Доказательство:

\(\frac{a}{b}\) и \(\frac{a+1}{b+1}\).

\( \frac{a}{b} ^{\color{blue}{\backslash b+1}} - \frac{a+1}{b+1} ^{\color{blue}{\backslash b}} =\)

\(=\frac{a(b+1) - b(a+1)}{b(b+1)}= \)

\(=\frac{\cancel{ab} + a - \cancel{ab} - b}{b(b+1)}= \)

\(=\frac{a - b}{b(b+1)}\).

\(b(b + 1) > 0\) при любом натуральном значении \(b\).

Вывод:

— Если \(a < b\), то \(a-b < 0\) и

\(\frac{a}{b} < \frac{a+1}{b+1}\) - дробь увеличивается.

— Если \(a > b\), то \(a-b > 0\) и

\(\frac{a}{b} > \frac{a+1}{b+1}\) - дробь уменьшается.

Пояснения:

1. Сравнение дробей свели к разности, которая равна \(\frac{a-b}{b(b+1)}\).

2. Так как \(b\) - натуральное число, знаменатель \(b(b+1) > 0\), поэтому знак дроби зависит только от знака разности \(a-b\).

3. Следовательно, при \(a < b\) дробь увеличивается, а при \(a > b\) дробь уменьшается.

а) \(a(a - 4) - a^2 > 12 - 6a\)

\(\cancel{a^2} - 4a - \cancel{a^2} > 12 - 6a\)

\(-4a > 12 - 6a \)

\(-4a + 6a > 12\)

\(2a > 12 \)   \(/ : 2\)

\(a > 6\)

Ответ: \((6; +\infty)\).

б) \((2x - 1)2x - 5x < 4x^2 - x\)

\((2x - 1)2x - 5x < 4x^2 - x \)

\(4x^2 - 2x - 5x < 4x^2 - x \)

\(4x^2 - 7x < 4x^2 - x\)

\(4x^2 - 7x - 4x^2 + x < 0 \)

\(-6x < 0 \)   \(/\times(-1)\)

\(x > 0\).

Ответ: \((0; +\infty)\).

в) \(5y^2 - 5y(y + 4) \geq 100\)

\(\cancel{5y^2} - \cancel{5y^2} - 20y \geq 100 \)

\(-20y \geq 100 \)   \(/ : (-20)\)

\(y \leq -5\).

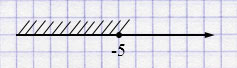
Ответ: \((-\infty; -5]\).

г) \(6a(a - 1) - 2a(3a - 2) < 6\)

\(\cancel{6a^2} - 6a - \cancel{6a^2} + 4a < 6\)

\(- 6a + 4a < 6 \)

\(-2a < 6 \)    \(/ : (-2)\)

\(a > -3\).

Ответ: \((-3; +\infty)\).

Пояснения:

При решении неравенств сначала раскрываем скобки, используя правило умножения одночлена на многочлен, и приводим подобные слагаемые.

Затем при решении неравенств используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.