Упражнение 682 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

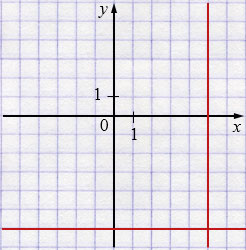
а) \((x-5)(y+6)=0 \)

\(x-5=0\)  или  \( y+6=0\)

\(x=5\)                 \(y=-6\)

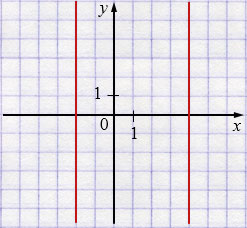
б) \((x-4)(x+2)=0 \)

\(x-4=0 \)  или  \(x+2=0 \)

\(x=4\)                 \( x=-2\)

Пояснения:

Использовано свойство нуля произведения: если \((A\cdot B)=0\), то \(A=0\) или \(B=0\). Поэтому уравнение с произведением двух линейных множителей задаёт объединение графиков двух линейных уравнений.

\(x = a\) - прямая, параллельная оси \(y\) и проходящая через точку с координатами \((a; 0)\).

\(y = b\) - прямая, параллельная оси \(x\) и проходящая через точку с координатами \((0; b)\).

\[x^2 + bx + c = 0\]

\(x_1 = b\), \(x_2 = c\)

По теореме Виета:

\( x_1 + x_2 = -b, \quad x_1 x_2 = c \)

Составим систему уравнений:

\( \begin{cases} b+c= -b,\\ bc = c \end{cases} \)

\( \begin{cases} c=-b -b,\\ bc - c = 0 \end{cases} \)

\( \begin{cases} c=-2b,\\ c(b - 1) = 0 \end{cases} \)

\(c = 0\) - не удовлетворяет условию \(c\neq0\)

 или \(b - 1=0\) 

        \(b = 1\)

\(c = -2\cdot1 = -2\)

Ответ: \(b = 1\), \(c = -2\).

Пояснения:

Так как корни уравнения совпадают с коэффициентами \(b\) и \(c\), мы использовали теорему Виета: \[ x_1 + x_2 = -b, \quad x_1 x_2 = c. \]

Подставив \(x_1 = b, x_2 = c\), получили систему:

\( \begin{cases} b+c= -b,\\ bc = c \end{cases} \)

Решив систему, получили

\(b = 1, c = -2\), при этом учли условие \(c \neq 0\) и исключили лишний корень