Упражнение 565 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

Пусть гипотенуза треугольника равна \(x\) см, тогда катеты \(x-3\) см  и \(x-6\) см.

По теореме Пифагора составим уравнение:

\((x-3)^2+(x-6)^2=x^2\)

\(x^2-6x+9+x^2-12x+36-x^2=0\)

\(x^2-18x+45=0\)

\(a=1\), \(b=-18\), \(c=45\).

\(D = b^2 - 4ac = 18^2-4\cdot1\cdot45=\)

\(=324-180=144\);     \(\sqrt D=12\).

\(x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-18)+12}{2}=\)

\(=\frac{30}{2}=15\).

\(x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-(-18) -12}{2}=\)

\(=\frac{6}{2}=3\) - не удовлетворяет условию \(x > 6\).

Ответ: гипотенуза равна 15 см.

Пояснения:

Использована теорема Пифагора:

\(\,a^2+b^2=c^2\),

где \(a\) и \(b\) - катеты прямоугольного треугольника, \(c\) - гипотенуза.

При обозначении гипотенузы \(x\) катеты равны \(x-3\) и \(x-6\), что даёт уравнение:

\((x-3)^2+(x-6)^2=x^2\).

При раскрытии скобок использовали формулу квадрата суммы и квадрата разности:

\((a+ b)^2 = a^2 + 2ab + b^2\);

\((a- b)^2 = a^2 - 2ab + b^2\).

Раскрыли скобки и перенесли слагаемое из правой части уравнения в левую со сменой знака, получили полное квадратное уравнение:

\(x^2-18x+45=0\).

Через дискриминант решили полученное уравнение и нашли два корня. Из двух корней остаётся \(x=15\), потому что гипотенуза должна быть больше обоих катетов, то есть \(x>6\).

Пусть сторона квадрата равна \(x\) см, тогда ширина доски также \(x\) см, а дина доски \(x + 20\) см. Площадь доски равна 4500 см².

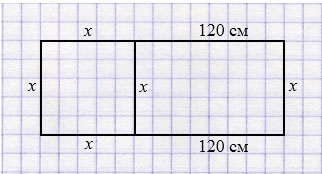
Составим уравнение:

\(x(x + 120) = 4500\)

\(x^2 + 120x - 4500 = 0\)

\(a=1\), \(b=120\), \(c=-4500\).

\(D = b^2 - 4ac = \)

\(=120^2 - 4\cdot1\cdot(-4500)=\)

\(=14400 + 18000 = 32 400\);

\(\sqrt{D} = 180\).

\(x_1 = \frac{-b + \sqrt{D}}{2a} =\frac{-120 + 180}{2\cdot1} =\)

\(=\frac{60}{2} = 30\).

\(x_2 = \frac{-b + \sqrt{D}}{2a} =\frac{-120 - 180}{2\cdot1} =\)

\(=\frac{300}{2} = -150\) - не удовлетворяет условию.

Ответ: сторона квадрата равна 30 см.

Пояснения:

Согласно условию ввели обозначения для длин сторон доски и, учитывая то, что площадь прямоугольника равна произведению его длины и ширины, составили уравнение:

\(x(x + 120) = 4500\).

Раскрыли скобки и перенесли слагаемое из правой части уравнения в левую со сменой знака, получили полное квадратное уравнение:

\(x^2 + 120x - 4500 = 0\).

Через дискриминант решили полученное уравнение и нашли два корня. Отрицательный корень не подходит, так как длина не может быть отрицательным числом. Положительный корень и есть искомая длина стороны квадрата.