Упражнение 334 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 80
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№334 учебника 2023-2025 (стр. 80):
Выберите из отмеченных точек те, которые соответствуют числам \(\sqrt{159}\) и \(\sqrt{127}\) (рис. 16).
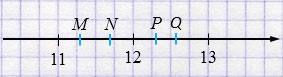
Рис. 16
№334 учебника 2013-2022 (стр. 80):
Найдите значение выражения:
а) \(\displaystyle \frac{1 - \frac{1}{x}}{1 + \frac{1}{x}}\) при \(x = -0{,}5\);
б) \(\displaystyle \frac{1}{1 + \frac{1}{1 + \frac{1}{x}}}\) при \(x = -0{,}4\).
Подсказка
№334 учебника 2023-2025 (стр. 80):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Умножение десятичных дробей.
- Положение чисел на координатной прямой.
№334 учебника 2013-2022 (стр. 80):
Вспомните:
- Рациональные дроби.
- Сложение и вычитание рациональных дробей с разными знаменателями.
- Умножение и деление рациональных дробей.
- Основное свойство рациональной дроби.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Сложение и вычитание десятичных дробей.
- Умножение десятичных дробей.
- Деление десятичных дробей.
Ответ
№334 учебника 2023-2025 (стр. 80):
1) \(\sqrt{159}\)
\(\sqrt{144}<\sqrt{159}<\sqrt{169}\)
\(12<\sqrt{159}<13\)
\(12,1^2 = 146,41\)
| × | 1 | 2 | 1 | ||
| 1 | 2 | 1 | |||
| + | 1 | 2 | 1 | ||
| 2 | 4 | 2 | |||
| 1 | 2 | 1 | |||
| 1 | 4 | 6 | 4 | 1 |
\(12,2^2 = 148,84\)
| × | 1 | 2 | 2 | ||
| 1 | 2 | 2 | |||
| + | 2 | 4 | 4 | ||
| 2 | 4 | 4 | |||
| 1 | 2 | 2 | |||
| 1 | 4 | 8 | 8 | 4 |
\(12,3^2 = 151,29\)
| × | 1 | 2 | 3 | ||
| 1 | 2 | 3 | |||
| + | 3 | 6 | 9 | ||
| 2 | 4 | 6 | |||
| 1 | 2 | 3 | |||
| 1 | 5 | 1 | 2 | 9 |
\(12,4^2 =153,76\)
| × | 1 | 2 | 4 | ||
| 1 | 2 | 4 | |||
| + | 4 | 9 | 6 | ||
| 2 | 4 | 8 | |||
| 1 | 2 | 4 | |||
| 1 | 5 | 3 | 7 | 6 |
\(12,5^2 =156,25\)
| × | 1 | 2 | 5 | ||
| 1 | 2 | 5 | |||
| + | 6 | 2 | 5 | ||
| 2 | 5 | 0 | |||
| 1 | 2 | 5 | |||
| 1 | 5 | 6 | 2 | 5 |
\(12,6^2 = 158,76\)
| × | 1 | 2 | 6 | ||
| 1 | 2 | 6 | |||
| + | 7 | 5 | 6 | ||
| 2 | 5 | 2 | |||
| 1 | 2 | 6 | |||
| 1 | 5 | 8 | 7 | 6 |
\(12,7^2 = 161,29\)
| × | 1 | 2 | 7 | ||
| 1 | 2 | 7 | |||
| + | 8 | 8 | 9 | ||
| 2 | 5 | 4 | |||
| 1 | 2 | 7 | |||
| 1 | 6 | 1 | 2 | 9 |
\(12,6<\sqrt{159}<12,7\) - соответствует точке Q.
2) \(\sqrt{127}\)
\(\sqrt{121}<\sqrt{127}<\sqrt{144}\)
\(11<\sqrt{127}<12\)
\(11,1^2 = 123,21\)
| × | 1 | 1 | 1 | ||
| 1 | 1 | 1 | |||
| + | 1 | 1 | 1 | ||
| 1 | 1 | 1 | |||
| 1 | 1 | 1 | |||
| 1 | 2 | 3 | 2 | 1 |
\(11,2^2 = 125,44\)
| × | 1 | 1 | 2 | ||
| 1 | 1 | 2 | |||
| + | 2 | 2 | 4 | ||
| 1 | 1 | 2 | |||
| 1 | 1 | 2 | |||
| 1 | 2 | 5 | 4 | 4 |
\(11,3^2 = 127,69\)
| × | 1 | 1 | 3 | ||
| 1 | 1 | 3 | |||
| + | 3 | 3 | 9 | ||
| 1 | 1 | 3 | |||
| 1 | 1 | 3 | |||
| 1 | 2 | 7 | 6 | 9 |
\(11,2<\sqrt{127}<11,3\) - соответствует точке М.
Ответ: \(Q(\sqrt{159})\), \(M(\sqrt{127})\).
Пояснения:
Арифметический квадратный корень из числа \(a\) — это такое неотрицательное число \(x\), при котором \(x^2 = a\).
№334 учебника 2013-2022 (стр. 80):
а) \( \frac{1 ^{\color{blue}{\backslash{x}}} - \frac{1}{x}}{1^{\color{blue}{\backslash{x}}} + \frac{1}{x}} =\frac{\frac{x - 1}{x}}{\frac{x + 1}{x}} =\)
\(=\frac{x - 1}{x} : \frac{x + 1}{x}=\)
\(=\frac{x - 1}{\cancel{x}} \cdot \frac{\cancel{x}}{x + 1}=\frac{x - 1}{x + 1}. \)
Если \(x = -0{,}5\), то
\(\frac{-0,5 - 1}{-0,5 + 1} = \frac{-1,5}{0,5} = \frac{-15}{5} = -3 \)
б) \( \frac{1}{1 + \frac{1}{1 ^{\color{blue}{\backslash{x}}} + \frac{1}{x}}} = \frac{1}{1 + \frac{1}{\frac{x + 1}{x}}} =\)
\(=\frac{1}{1 ^{\color{blue}{\backslash{x+1}}} + \frac{x}{x + 1}} = \frac{1}{\frac{x + 1 + x}{x + 1}} =\)
\(=\frac{x + 1}{2x + 1}. \)
Если \(x = -0{,}4\), то
\(\frac{-0,4 + 1}{2\cdot(-0,4) + 1}=\frac{0,6}{-0,8 + 1}= \)
\(=\frac{0,6}{0,2} = \frac62 = 3\).
Пояснения:
Использованные приёмы:
1) Черту дроби можно заменить делением: числитель разделить на знаменатель.
2) Для сложения и вычитания дробей приводим их к общему знаменателю, умножая числитель и знаменатель каждой дроби на необходимые множители.
3) Деление дробей выполняется умножением на обратную дробь:
\(\frac{A}{B} : \frac{C}{D} = \frac{A}{B}\cdot\frac{D}{C}= \frac{A\cdot D}{B\cdot C}.\)
4) Чтобы найти значение буквенного выражения при заданных числовых значениях переменных, нужно вместо переменных в это выражение подставить числа и выполнить вычисления.
Вернуться к содержанию учебника