Упражнение 335 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 80
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№335 учебника 2023-2025 (стр. 80):
Сравните с нулём значение выражения:
а) \(\sqrt{7} - 3\);
б) \(11 - \sqrt{107}\);
в) \(\sqrt{85} - 4\);
г) \(19 - \sqrt{326}\);
д) \(15 - \sqrt{225}\);
е) \(\sqrt{625} - 25\).
№335 учебника 2013-2022 (стр. 80):
Изобразите схематически в одной и той же системе координат графики функций \(y = \frac{10}{x}\) и \(y = 10x\). Имеют ли эти графики общие точки, и если имеют, то сколько?
Подсказка
№335 учебника 2023-2025 (стр. 80):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Сравнение натуральных чисел.
- Степень с натуральным показателем.
№335 учебника 2013-2022 (стр. 80):
Ответ
№335 учебника 2023-2025 (стр. 80):
а) \(\sqrt{7} - 3 =\sqrt{7} - \sqrt{9} < 0\),
так как \(\sqrt{7}<\sqrt{9}\).
б) \(11 - \sqrt{107} =\sqrt{121} - \sqrt{107} > 0\),
так как \(\sqrt{121} > \sqrt{107}\).
в) \(\sqrt{85} - 4 = \sqrt{85} - \sqrt{16} > 0\),
так как \(\sqrt{85} > \sqrt{16}\).
г) \(19 - \sqrt{326} = \sqrt{361} - \sqrt{326} > 0\),
так как \(\sqrt{361} > \sqrt{326}\).
д) \(15 - \sqrt{225} = 15 - 15 = 0\).
е) \(\sqrt{625} - 25 = 25 - 25 = 0\).
Пояснения:
Использованные правила и приёмы:
Если \(a = \sqrt{x}\), то \(x = a^2\).
Для положительных \(a\) и \(b\):
если \(a>b\), то \(\sqrt{a}>\sqrt{b}\).
№335 учебника 2013-2022 (стр. 80):
\(y=\frac{10}{x}\) - гипербола.
\(y=10x\) - прямая.
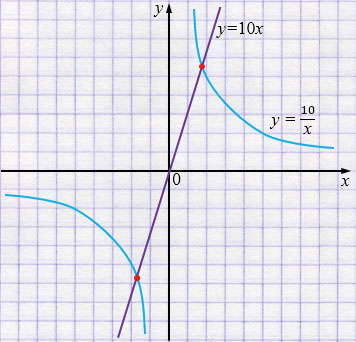
Ответ: графики имеют две общие точки.
Пояснения:
1) График \(y=10x\) — возрастающая прямая, проходящая через начало координат.
2) График \(y=\frac{10}{x}\) — гипербола, ветви которой находятся в I и III координатных четвертях.
Вернуться к содержанию учебника