Упражнение 287 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№287 учебника 2023-2025 (стр. 70):
Известно, что график функции \(y = \dfrac{k}{x}\) проходит через точку \(A(4;\ -0{,}5)\). Найдите \(k\) и постройте этот график.
№287 учебника 2013-2022 (стр. 72):
Какие целые числа расположены между числами:
а) \(-3{,}168\ldots\) и \(2{,}734\ldots\);
б) \(-5{,}106\ldots\) и \(-1{,}484\ldots\);
в) \(-4{,}06\) и \(-1{,}601\);
г) \(-1{,}29\) и \(0{,}11\)?
Подсказка
№287 учебника 2023-2025 (стр. 70):
Вспомните:
- График обратной пропорциональности.
- Координаты точки.
- Деление и дроби.
- Деление рациональных чисел.
- Деление десятичных дробей.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Умножение десятичных дробей.
- Линейное уравнение с одной переменной, его свойства.
№287 учебника 2013-2022 (стр. 72):
Вспомните:
- Положение чисел на координатной прямой, целые числа.
- Сравнение рациональных чисел.
- Сравнение десятичных дробей.
Ответ
№287 учебника 2023-2025 (стр. 70):
\(y = \dfrac{k}{x}\)
\(A(4;\ -0{,}5)\)
\(-0,5 = \dfrac{k}{4}\) /\(\times4\)
\(k = -2\)
\(y = -\dfrac{2}{x}\)
| \(x\) | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 |
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
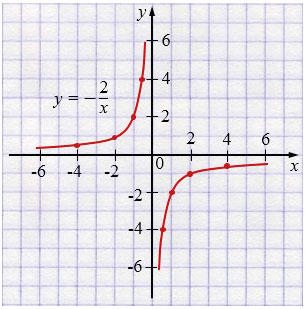
Пояснения:
Использованные правила и приёмы:
• Функция обратной пропорциональности задаётся формулой \(y=\dfrac{k}{x}\).
• Число \(k\) находим, подставляя координаты данной точки в функцию \(y=\dfrac{k}{x}\) вместо \(x\) и \(y\).
• После вычисления \(k\) записываем итоговое уравнение \(y=\frac{k}{x}\).
При решении уравнения, чтобы найти \(k\), обе части уравнения умножили на знаменатель дроби.
• Графиком обратной пропорциональности \(y=\frac{k}{x}\) является гипербола (две ветви). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
№287 учебника 2013-2022 (стр. 72):
а) Целые числа между \(-3{,}168\ldots\) и \(2{,}734\ldots\):
\(-3,\ -2,\ -1,\ 0,\ 1,\ 2\)
б) Целые числа между \(-5{,}106\ldots\) и \(-1{,}484\ldots\):
\(-5,\ -4,\ -3,\ -2\)
в) Целые числа между \(-4{,}06\) и \(-1{,}601\):
\(-4,\ -3,\ -2\)
г) Целые числа между \(-1{,}29\) и \(0{,}11\):
\(-1,\ 0\)
Пояснения:
Чтобы определить, какие целые числа находятся между двумя числами, нужно:
1. Округлить левую границу до ближайшего большего целого (если число не целое).
2. Округлить правую границу до ближайшего меньшего целого (если число не целое).
3. Все целые числа между этими двумя округлениями входят в ответ.
Вернуться к содержанию учебника