Упражнение 1163 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 259
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№1163 учебника 2023-2025 (стр. 259):
Постройте график функции \(y=\dfrac{4x+3}{4x^{2}+3x}\). Определите, при каких значениях \(k\) прямая \(y=kx\) имеет с графиком ровно одну общую точку.
Подсказка
№1163 учебника 2023-2025 (стр. 259):
Вспомните:
- Рациональные дроби.
- Основное свойство рациональной дроби (сокращение дробей).
- Вынесение общего множителя за скобки.
- Функция обратной пропорциональности, ее график.
- Линейная функция, ее график.
- Координаты точки на координатной плоскости.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Неправильные дроби.
- Смешанные числа.
- Деление рациональных чисел.
- Деление обыкновенных дробей.
- Умножение обыкновенных дробей.
Ответ
№1163 учебника 2023-2025 (стр. 259):
\( y=\frac{4x+3}{4x^{2}+3x}=\frac{4x+3}{x(4x+3)}=\frac{1}{x}\)
ОДЗ: \(x\ne0\) и \(4x+3 \ne 0\)
\(4x \ne -3\)
\(x\ne-\frac34\)
\(y=\dfrac1x\) - гипербола.
| \(x\) | 0,25 | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 | 0,25 |
| \(x\) | -0,25 | -0,5 | -1 | -2 | -4 |
| \(y\) | -4 | -2 | -1 | -0,5 | -0,25 |
Если \(x = -\frac34\), то \(y =\frac{1}{-\frac34}= -\frac43\).
\(\Bigl(-\dfrac34,-\dfrac43\Bigr)\) - выколотая точка.
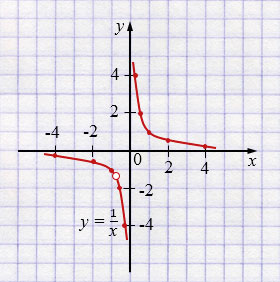
Прямая \(y = kx\) имеет с графиком функции \( y=\frac{4x+3}{4x^{2}+3x}\) одну общую точку, если она проходит через точку \(\Bigl(-\dfrac34,-\dfrac43\Bigr)\), тогда
\(-\dfrac43 = k \cdot \Bigl(-\dfrac34\Bigr)\)
\(k = -\dfrac43 : \Bigl(-\dfrac34\Bigr)\)
\(k = \dfrac43 \cdot \dfrac43\)
\(k = \dfrac{16}{9}\)
\(k = 1\dfrac{7}{9}\)
Ответ: прямая \(y = kx\) имеет с графиком функции \( y=\frac{4x+3}{4x^{2}+3x}\) одну общую точку при \(k = 1\dfrac{7}{9}\).
Пояснения:
Чтобы построить график заданной функции сначала, нужно выполнить преобразования (сократить дробь), учитывая ОДЗ (область допустимых значений).
В результате преобразований получили функцию \(y=\dfrac1x\) - график гипербола, ветви которой расположены в 1 и 3 координатной четвертях, так как \(k = 1 > 0\). Построили график по точкам, причем точку, у которой \(x\ne-\frac34\) сделали выколотой, так как функция в этой точке не существует.
Графиком функции \(y = kx\) является прямая, проходящая через начало координат.
При \(k <0\) прямая \(y = kx\) будет проходит через 2 и 4 координатные четверти и в этом случае общих точек с графиком функции \( y=\frac{4x+3}{4x^{2}+3x}\).
При \(k > 0\) прямая \(y = kx\) будет проходит через 1 и 3 координатные четверти и в этом случае будет иметь две общие точки с графиком функции \( y=\frac{4x+3}{4x^{2}+3x}\), кроме того случая, когда прямая \(y=kx\) проходит через точку \(\Bigl(-\dfrac34,-\dfrac43\Bigr)\) - в этом случае общая точка будет одна при \(k = 1\dfrac{7}{9}\) (смотри решение выше).
Вернуться к содержанию учебника