Упражнение 1215 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

а) \((x - 2)(y + 3) = 0\)

1) \(x - 2 = 0\)

\(x = 2\).

2) \(y + 3 = 0\).

\(y = -3\).

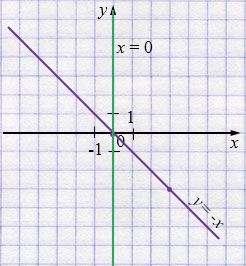
б) \(x^2 + x y = 0\)

\( x(x + y) = 0 \)

1) \(x = 0\) - ось \(y\).

2) \(x + y = 0\).

\(y = -x\)

Пояснения:

Уравнение вида произведения равно нулю разбивается на несколько линейных уравнений, каждое задаёт прямую.

а) Уравнение \((x - 2)(y + 3) = 0\) означает, что либо \(x - 2 = 0\), либо \(y + 3 = 0\).

— Прямая \(x = 2\);

— Прямая \(y = -3\).

Получились две перпендикулярные прямые \(x=2\) - вертикальная прямая и \(y=-3\) - горизонтальная прямая.

б) Уравнение \(x^2 + x y = 0\) можно разложить:

\( x(x + y) = 0 \)

Значит либо \(x = 0\), либо \(x + y = 0\).

— Прямая \(x = 0\) (ось \(y\));

— Прямая \(y = -x\).

График: прямые \(x=0\), то есть ось \(y\), и \(y=-x\) пересекаются в начале координат.

Составим систему уравнений:

\( \begin{cases} 19^3a + 19^2b + 19c + d = 1,  /\times(-1) \\ 62^3a + 62^2b + 62c + d = 2 \end{cases} \)

\( \begin{cases} -19^3a - 19^2b - 19c - d = 1, \\ 62^3a + 62^2b + 62c + d = 2 \end{cases} \) \((+)\)

\((62^3 - 19^3)\,a +(62^2 - 19^2)\,b+(62 - 19)\,c = 1\)

\((62 - 19)(62^2 - 62\cdot19 + 19^2)\,a +(62 - 19)(62 + 19)\,b+43\,c = 1\)

\(43(62^2 - 62\cdot19 + 19^2)\,a + 43(62 + 19)\,b+43\,c = 1\)  / \(:43\)

\((62^2 - 62\cdot19 + 19^2)\,a + (62 + 19)\,b+c = \frac{1}{43}\) - дробное число.

Значит, коэффициенты \((a,b,c,d)\) не могут быть целыми числами.

Что и требовалось доказать.

Пояснения:

– Мы составили систему для неизвестных коэффициентов, домножили первое уравнение системы на (-1) и, сложив уравнения системы, исключили свободный член \(d\).

– По формулам разности кубов и разности квадратов, получили то, что каждое слагаемое в левой части уравнения имеет множитель 43, значит, левая часть уравнения делится нацело на 43, но справа стоит единица, которая нацело на 43 не делится. Значит, коэффициенты \((a,b,c,d)\) не могут быть целыми числами.

Разность кубов:

\(a^3 - b^3 = (a-b)(a^2 + ab + b^2\).

Разность квадратов:

\(a^2 - b^2 = (a - b)(a + b)\).