Сумма и разность кубов двух выражений / Формулы сокращенного умножения / Алгебра / Справочник по математике 5-9 класс

Сумма кубов двух выражений

Найдем произведение двучлена 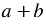и трехчлена 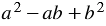. Согласно правилу умножения многочлена на многочлен, получим:

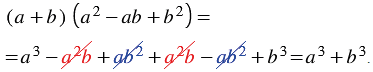
Итак, мы получили тождество:

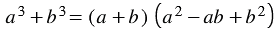, которое называют формулой суммы кубов двух выражений.

Многочлен 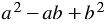, стоящий в правой части, похож на многочлен 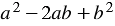, который равен квадрату разност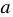и и 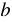, поэтому многочлен 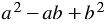называют неполным квадратом разности.

Правило:

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Пример:

Разложите на множители многочлен .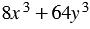

Решение:

Используя свойства степени, представляем данный многочлен в виде суммы кубов двух выражений, получаем:

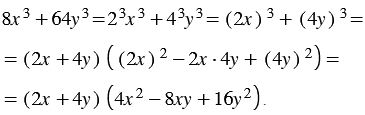
Разность кубов двух выражений

Найдем произведение двучлена 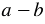и трехчлена 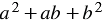. Согласно правилу умножения многочлена на многочлен, получим:

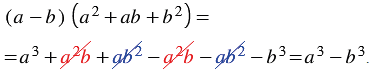
Итак, мы получили тождество:

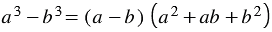, которое называют формулой разности кубов двух выражений.

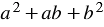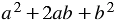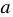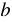Многочлен , стоящий в правой части, похож на многочлен , который равен квадрату суммы и , поэтому многочлен 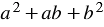называют неполным квадратом суммы.

Правило:

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Пример:

Разложите на множители многочлен .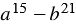

Решение:

Используя свойства степени, представляем данный многочлен в виде разности кубов двух выражений, получаем:

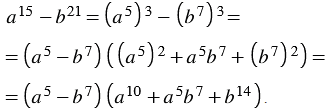
Советуем посмотреть:

Произведение разности и суммы двух выражений. Разность квадратов двух выражений.

Квадрат суммы и квадрат разности двух выражений

Введение в алгебру

Линейное уравнение с одной переменной

Решение задач с помощью уравнений

Тождественно равные выражения. Тождества

Степень с натуральным показателем

Свойства степени с натуральным показателем

Одночлены

Многочлены

Сложение и вычитание многочленов

Умножение одночлена на многочлен

Умножение многочлена на многочлен

Разложение многочленов на множители

Формулы сокращенного умножения

Рациональные выражения

Функции

Квадратные корни. Дейстительные числа

Квадратные уравнения

Системы линейных уравнений с двумя переменными

Элементы математической логики

Алгебра

Правило встречается в следующих упражнениях:

7 класс

Номер 682, Мерзляк, Полонский, Якир, Учебник

Номер 686, Мерзляк, Полонский, Якир, Учебник

Номер 688, Мерзляк, Полонский, Якир, Учебник

Номер 689, Мерзляк, Полонский, Якир, Учебник

Номер 691, Мерзляк, Полонский, Якир, Учебник

Номер 699, Мерзляк, Полонский, Якир, Учебник

Номер 716, Мерзляк, Полонский, Якир, Учебник

Номер 721, Мерзляк, Полонский, Якир, Учебник

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 1, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 24, Мерзляк, Полонский, Якир, Учебник

Номер 36, Мерзляк, Полонский, Якир, Учебник

Номер 48, Мерзляк, Полонский, Якир, Учебник

Номер 76, Мерзляк, Полонский, Якир, Учебник

Номер 6, Мерзляк, Полонский, Якир, Учебник

Номер 286, Мерзляк, Полонский, Якир, Учебник

Номер 287, Мерзляк, Полонский, Якир, Учебник

Номер 769, Мерзляк, Полонский, Якир, Учебник

Номер 791, Мерзляк, Полонский, Якир, Учебник

Номер 862, Мерзляк, Полонский, Якир, Учебник