Упражнение 1129 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1129 учебника 2023-2025 (стр. 223):
За 3 ч по течению и 4 ч против течения теплоход проходит 380 км. За 1 ч по течению и 30 мин против течения теплоход проходит 85 км. Найдите собственную скорость теплохода и скорость течения.
№1129 учебника 2013-2022 (стр. 225):
Покажите штриховкой множество точек координатной плоскости, которое задаёт неравенство:
а) \(y \ge x\);
б) \(y \le -x\);
в) \(x \ge 1\);
г) \(y \le 5\).
Подсказка
№1129 учебника 2023-2025 (стр. 223):
Вспомните:
- Решение задач с помощью системы уравнений.
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Распределительное свойство умножения.
- Подобные слагаемые.
№1129 учебника 2013-2022 (стр. 225):
Вспомните:
Ответ
№1129 учебника 2023-2025 (стр. 223):
30 мин = 0,5 ч
Пусть \(x\) (км/ч) собственная скорость теплохода, а \(y\) (км/ч) - скорость течения. Тогда скорость по течению равна \(x+y\) (км/ч), а против течения — \(x - y\) (км/ч).
Составим систему уравнений:
\( \begin{cases} 3(x+y)+4(x-y)=380,\\ 1\cdot(x+y)+0{,}5\,(x-y)=85. \end{cases} \)
\( \begin{cases} 3x+3y+4x-4y=380,\\ x+y+0{,}5x-0{,}5y=85. \end{cases} \)
\( \begin{cases} 7x-y=380,\\ 1{,}5x+0{,}5y=85 / : 0,5 \end{cases} \)
\( \begin{cases} 7x-y=380,\\ 3x+y=170 \end{cases} \)
\( \begin{cases} 10x=550,\\ 3x+y=170 \end{cases} \)
\( \begin{cases} x=\frac{550}{10},\\ y=170 -3x \end{cases} \)
\( \begin{cases} x=55,\\ y=170-3\cdot55 \end{cases} \)
\( \begin{cases} x=55,\\ y=170-165 \end{cases} \)
\( \begin{cases} x=55,\\ y=5 \end{cases} \)
Ответ: собственная скорость теплохода 55 км/ч и скорость течения 5 км/ч.
Пояснения:
Использованные приёмы:
1) Введение переменных: \(x\) — собственная скорость лодки, \(y\) — скорость течения.
2) Составление системы уравнений. Чтобы найти расстояние, нужно скорость движения умножить на время в пути.
3) Раскрытие скобок, используя распределительное свойство умножения:
\(a(b+c)=ab+ac\).
4) Приведение подобных членов при преобразовании каждого уравнения:
\(ax + bx = (a + b)x\).
5) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
6) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
7) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
8) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
№1129 учебника 2013-2022 (стр. 225):
а) \(y \ge x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |

б) \(y \le -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
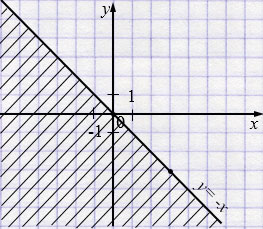
в) \(x \ge 1\)

г) \(y \le 5\)

Пояснения:
1) Для неравенства вида \(y \ge kx + b\) или \(y \le kx + b\) проводят границу линию и закрашивают полуплоскость, где неравенство истинно. Если знак «\(\ge\)» или «\(\le\)», граница включается (штриховка до линии).
2) Для неравенств \(x \ge c\) или \(x \le c\) проводят вертикальную линию \(x=c\) и штрихуют соответствующую полуплоскость (справа или слева от прямой).
3) Аналогично для \(y \ge c\) или \(y \le c\) проводят горизонтальную линию \(y=c\) и штрихуют область выше или ниже неё.
а) \(y \ge x\): прямая \(y=x\) — граница. Штриховка области над и на этой прямой. Точки на прямой включаются.
б) \(y \le -x\): прямая \(y=-x\) — граница. Штриховка области под и на этой прямой (слева-внизу). Точки на прямой включаются.
в) \(x \ge 1\): вертикальная прямая \(x=1\). Штриховка области справа от неё (включая саму линию).
г) \(y \le 5\): горизонтальная прямая \(y=5\). Штриховка области ниже неё (включая саму линию).
Вернуться к содержанию учебника