Упражнение 757 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 158
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№757 учебника 2023-2025 (стр. 158):
Докажите, что при любом значении \(a\) сумма многочленов
\(\;1{,}6a^5 - 1\tfrac{1}{3}a^4 - 3{,}4a^3 - a^2 - 1\)
и
\(-1\tfrac{3}{5}a^5 - \tfrac{2}{3}a^4 + 3\tfrac{2}{5}a^3\)
принимает отрицательное значение.
№757 учебника 2013-2022 (стр. 158):
Расстояние между пристанями \(M\) и \(N\) равно 162 км. От пристани \(M\) отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани \(N\) навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?
Подсказка
№757 учебника 2023-2025 (стр. 158):
Вспомните:
- Что называют многочленом.
- Сложение и вычитание многочленов.
- Подобные слагаемые, раскрытие скобок.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Десятичная запись дробных чисел.
- Сложение и вычитание десятичных дробей.
- Сложение обыкновенных дробей.
- Неправильные дроби.
- Степень с натуральным показателем.
- Сравнение рациональных чисел.
№757 учебника 2013-2022 (стр. 158):
Вспомните:
- Решение задач с помощью уравнений.
- Линейное уравнение.
- Подобные члены.
- Задачи на движение.
- Деление и дроби.
- Умножение одночлена на многочлен.
- Распределительное свойство умножения.
- Умножение десятичных дробей.
- Сокращение дробей.
- Неправильные дроби.
- Смешанные числа.
- Единицы измерения времени.
Ответ
№757 учебника 2023-2025 (стр. 158):
\( \bigl(1{,}6a^5 - 1\tfrac{1}{3}a^4 - 3{,}4a^3 - a^2 - 1\bigr) +\bigl(-1\tfrac{3}{5}a^5 - \tfrac{2}{3}a^4 + 3\tfrac{2}{5}a^3\bigr)= \)
\(=1,6a^5 - 1\tfrac{1}{3}a^4 - 3,4a^3 - a^2 -1 -1,6a^5 - \tfrac{2}{3}a^4 + 3,4a^3= \)
\(=(1,6a^5 -1,6a^5) - (\tfrac{2}{3}a^4 + 1\tfrac{1}{3}a^4) + (3,4a^3 - 3,4a^3) - a^2 - 1=\)
\(= -2a^4 - a^2 - 1 =\)
\(=-\bigl(2a^4 + a^2 + 1\bigr) < 0 \) при любом значении \(a\).
Пояснения:
1. Обнуление членов высших степеней. Коэффициенты при \(a^5\) и \(a^3\) взаимно уничтожились.
2. Выделение отрицательного множителя. Полученный многочлен записан как \(-\bigl(2a^4 + a^2 + 1\bigr)\).
3. Положительность внутренней суммы. Для любого \(a\) верно \(2a^4\ge0\) и \(a^2\ge0\), поэтому \(2a^4 + a^2 + 1 > 0\).
4. Заключение. Произведение \(-1\) на положительное число дает отрицательное значение, следовательно исходная сумма всегда отрицательна при любом \(a\).
№757 учебника 2013-2022 (стр. 158):
\(45\) мин = \( \tfrac{45}{60} = \tfrac{3}{4} = 0,75\) ч
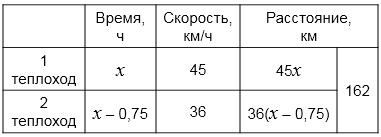
Составим уравнение:
\( 45x + 36\,(x - 0{,}75) = 162\)
\( 45x + 36x - 27 = 162\)
\(81x = 162 + 27\)
\( 81x = 189\)
\(x = \tfrac{{\cancel{189}}^{7}}{{\cancel{81}}^{3}}\)
\(x = \tfrac{7}{3} \)
\(x = 2\tfrac{1}{3} \) (ч) = 2 ч 20 мин.
Ответ: через 2 ч 20 мин после отправления первого теплохода они встретятся.
Пояснения:
Использованные правила и приёмы:
1. Переход от минут к долям часа:
\(45\text{ мин}=0{,}75\) ч.
2. Формула движения: \(S = v\,t\) - чтобы найти расстояние, нужно скорость умножить на время.
3. При встречном движении суммы пройденных расстояний дают общее расстояние.
4. Раскрытие скобок:
\(a(b + c) = ab + ac\),
\(a(b - c) = ab - ac\).
5. Перенос подобных членов из одной части уравнения в другую со сменой знака.
\(A + C= B + D\), то
\(A - D = B - C\).
6. Приведение подобных членов
\(ka + la = (k + l)a\).
7. Решение линейного уравнения, учитывая то, что из линейного уравнения \(ax = b\) следует \(x = \tfrac{b}{a}\) при \(a\neq0\).
Пояснения по шагам:
– Ввели \(x\) как время до встречи первого теплохода.
– Учли, что второй теплоход идёт
\(x - 0{,}75\) ч.
– Составили уравнение по сумме пройденных ими расстояний:
\(45x + 36(x-0{,}75)=162\).
– Раскрыли скобки, перенесли и привели подобные члены, решили линейное уравнение и получили
\(x=\tfrac{7}{3}\) ч.
Вернуться к содержанию учебника