Упражнение 678 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№678 учебника 2023-2025 (стр. 145):
Найдите корни уравнения:
а) \(5x^2 + 3x = 0\);
б) \(x^2 - 11x = 0\);
в) \(6x^2 - 3{,}6x = 0\);
г) \(0{,}3x^2 - 3x = 0\);
д) \(5x^2 - 0{,}8x = 0\);
е) \(7x^2 - 0{,}28x = 0\).
№678 учебника 2013-2022 (стр. 147):
Упростите выражение:
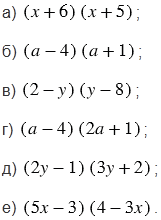
Подсказка
№678 учебника 2023-2025 (стр. 145):
Вспомните:
№678 учебника 2013-2022 (стр. 147):
Вспомните:
- Что называют многочленом.
- Умножение многочлена на многочлен.
- Умножение рациональных чисел.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
Ответ
№678 учебника 2023-2025 (стр. 145):
а) \(5x^2 + 3x =0;\)
\(x(5x + 3) = 0;\)
\(x=0\) или \(5x + 3= 0;\)
\(5x =- 3;\)
\(x =-\frac35;\)
Ответ: \(x = 0\), \(x = -\frac{3}{5}\).
б) \(x^2 - 11x =0;\)
\(x(x - 11) = 0;\)
\(x=0\) или \(x - 11 = 0;\)
\(x =11;\)
Ответ: \(x = 0\), \(x = 11\).
в) \(6x^2 - 3{,}6x =0;\)
\(x(6x - 3{,}6) = 0;\)
\(x=0\) или \(6x - 3{,}6 = 0;\)
\(6x = 3{,}6;\)
\(x = \frac{3{,}6}{6};\)
\(x =0,6;\)
Ответ: \(x = 0\), \(x = 0{,}6\).
г) \(0{,}3x^2 - 3x =0;\)
\(x(0{,}3x - 3) = 0;\)
\(x=0\) или \(0{,}3x - 3 = 0;\)
\(0{,}3x =3;\)
\(x =\frac{3}{0{,}3};\)
\(x =10;\)
Ответ: \(x = 0\), \(x = 10\).
д) \(5x^2 - 0{,}8x =0;\)
\(x(5x - 0{,}8) = 0;\)
\(x=0\) или \(5x - 0{,}8 = 0;\)
\(5x =0{,}8;\)
\(x=\frac{0{,}8}{5};\)
\(x=0,16;\)
| - | 0 | 8 | 5 | ||||
| 5 | 0 | 1 | 6 | ||||
| - | 3 | 0 | |||||
| 3 | 0 | ||||||
| 0 |
Ответ: \(x = 0\), \(x = 0{,}16\).
е) \(7x^2 - 0{,}28x =0;\)
\(x(7x - 0{,}28) = 0;\)
\(x=0\) или \(7x - 0{,}28= 0;\)
\(7x = 0{,}28;\)
\(x = \frac{0{,}28}{7};\)
\(x = 0{,}04\).
Ответ: \(x = 0\), \(x = 0{,}04\).
Пояснения:
Использованные правила:
1) Распределительный закон:
\[a(b +c) =ab+ac\]
2) Обратный распределительный закон (вынос общего множителя):
\[ab+ac =a(b +c)\]
3) Свойство множителя −1:
\[-k·x = -kx\] и \[-1·(x + y) = -(x + y)\]
4) Свойство нулевого произведения:
\[AB = 0 \;\Longrightarrow\; A = 0 \;\text{или}\; B = 0\]
Для каждого уравнения выделили общий множитель (переменную или её степень), затем применили свойство нулевого произведения: приравняли каждый множитель к нулю и нашли все корни.
№678 учебника 2013-2022 (стр. 147):
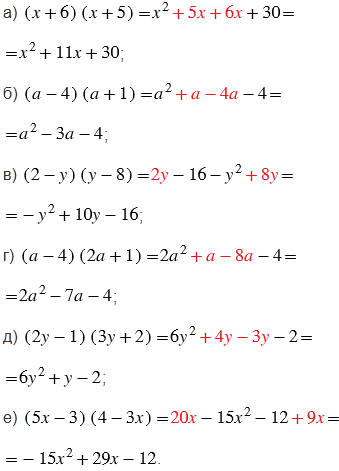
Пояснения:
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить (мы говорим об алгебраической сумме - выражение, которое можно представить в виде суммы положительных и отрицательных чисел). В решении выделены одинаковым цветом подобные слагаемые, их мы складываем (вычитаем), тем самым упрощая выражение.
Вернуться к содержанию учебника