Упражнение 1170 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

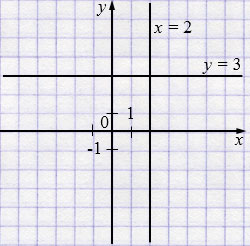
а) \((x - 2)(y - 3) = 0\)

\(x - 2 = 0\)

\(x = 2\)

или \(y - 3 = 0\)

\(y = 3\).

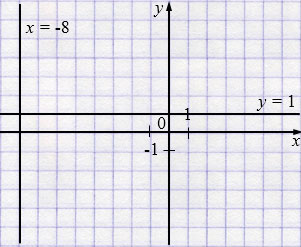
б) \((x + 8)(y - 1) = 0\)

\(x + 8 = 0\)

\(x = -8\)

или \(y - 1 = 0\)

\(y = 1\)

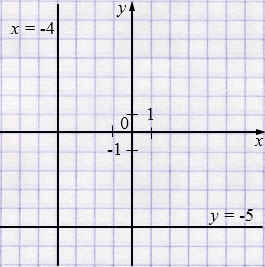
в) \((x + 4)(y + 5) = 0\)

\(x + 4 = 0\)

\(x = -4\)

или \(y + 5 = 0\)

\(y = -5\)

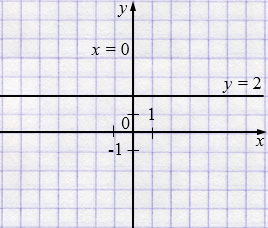
г) \(x(y - 2) = 0\)

\(x = 0\) - ось \(y\);

или \(y - 2 = 0\)

\(y = 2\)

Пояснения:

– Уравнение вида \((x-a)(y-b)=0\) на плоскости задаёт две прямые \(x-a=0\) и \(y-b=0\).

– Каждое из уравнений вида \(x = a\) — вертикальная прямая, а вида \(y = b\) — горизонтальная, где \(a\) и \(b\) - некоторые числа.

– Для построения прямой \(x = a\) достаточно отметить любую точку с абсциссой \(a\), а для \(y = b\) — с ординатой \(b\).

– В каждом пункте график состоит из двух перпендикулярных прямых, пересекающихся в их общей точке.

а) \( \begin{cases} \frac{x}{5} = 1 - \frac{y}{15},   /\times15\\ 2x - 5y = 0; \end{cases} \)

\( \begin{cases} 3x = 15 - y, \\ 2x - 5y = 0; \end{cases} \)

\( \begin{cases} 3x + y = 15,   /\times5 \\ 2x - 5y = 0; \end{cases} \)

\( \begin{cases} 15x + 5y = 75, \\ 2x - 5y = 0; \end{cases} \)     \((+)\)

\( \begin{cases} 17x = 75, \\ 2x - 5y = 0; \end{cases} \)

\( \begin{cases} x = \frac{75}{17}, \\ 5y = 2x; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ 5y = 2\cdot\frac{75}{17}; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ 5y = \frac{150}{17}; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ y = \frac{150}{17} : 5; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ y = \frac{^{30}\cancel{150}}{17} \cdot \frac{1}{\cancel5}; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ y = \frac{30}{17}; \end{cases} \)

\( \begin{cases} x = 4\frac{7}{17}, \\ y = 1\frac{13}{17}; \end{cases} \)

Ответ: \(x=4\frac{7}{17}\), \(y = 1\frac{13}{17}\).

б) \( \begin{cases} 3m + 5n = 1,\\ \frac{m}{4} + \frac{3n}{5} = 1;  /\times20 \end{cases} \)

\( \begin{cases} 3m + 5n = 1,  /\times(-5) \\ 5m + 12n = 20;  /\times3 \end{cases} \)

\( \begin{cases} -15m - 25n = -5, \\ 15m + 36n = 60; \end{cases} \)      \((+)\)

\( \begin{cases} 11n = 55, \\ 15m + 36n = 60; \end{cases} \)

\( \begin{cases} n = \frac{55}{11}, \\ 15m = 60 - 36n; \end{cases} \)

\( \begin{cases} n = 5, \\ 15m = 60 - 36\cdot5; \end{cases} \)

\( \begin{cases} n = 5, \\ 15m = 60 - 180; \end{cases} \)

\( \begin{cases} n = 5, \\ 15m = -120; \end{cases} \)

\( \begin{cases} n = 5, \\ m = -\frac{120}{15}; \end{cases} \)

\( \begin{cases} n = 5, \\ m = -8; \end{cases} \)

 Ответ: \(m = -8\), \(n = 5\).

в) \( \begin{cases} 4x - 3y = 1,\\ \frac{2x + 1}{6} = \frac{9 - 5y}{8};  /\times24 \end{cases} \)

\( \begin{cases} 4x - 3y = 1,\\ 4(2x + 1) = 3(9 - 5y); \end{cases} \)

\( \begin{cases} 4x - 3y = 1,\\ 8x + 4 = 27 - 15y; \end{cases} \)

\( \begin{cases} 4x - 3y = 1,  /\times(-2) \\ 8x + 15y = 27 - 4; \end{cases} \)

\( \begin{cases} -8x + 6y = -2, \\ 8x + 15y = 23; \end{cases} \)      \((+)\)

\( \begin{cases} 21y = 21, \\ 8x + 15y = 23; \end{cases} \)

\( \begin{cases} y = 1, \\ 8x = 23 - 15y; \end{cases} \)

\( \begin{cases} y = 1, \\ 8x = 23 - 15\cdot1; \end{cases} \)

\( \begin{cases} y = 1, \\ 8x = 8; \end{cases} \)

\( \begin{cases} y = 1, \\ x = 1. \end{cases} \)

Ответ: \(x =1\), \(y=1\).

г) \( \begin{cases} 3q = 4p - 7,\\ \frac{1 - 3q}{4} = \frac{4 - 2p}{3};  /\times12 \end{cases} \)

\( \begin{cases} 3q - 4p = -7,\\ 3(1 - 3q) = 4(4 - 2p); \end{cases} \)

\( \begin{cases} 3q - 4p = -7,\\ 3 - 9q = 16 - 8p; \end{cases} \)

\( \begin{cases} 3q - 4p = -7,   /\times3 \\ -9q + 8p = 16 - 3; \end{cases} \)

\( \begin{cases} 9q - 12p = -21, \\ -9q + 8p = 13; \end{cases} \)     \((+)\)

\( \begin{cases} -4p = -8, \\ -9q + 8p = 13; \end{cases} \)

\( \begin{cases} p = \frac{8}{4}, \\ 9q = 8p - 13; \end{cases} \)

\( \begin{cases} p = 2, \\ 9q = 8\cdot2 - 13; \end{cases} \)

\( \begin{cases} p = 2, \\ 9q = 3; \end{cases} \)

\( \begin{cases} p = 2, \\ q = \frac39; \end{cases} \)

\( \begin{cases} p = 2, \\ q = \frac13. \end{cases} \)

Ответ: \(p = 2, \) \( q = \frac13.\)

Пояснения:

Использованные приёмы:

1) Преобразование уравнений к целым коэффициентам умножением на общий знаменатель дробей, входящих в уравнение.

2) Перенос членов из одной части уравнения в другую:

если \(a+b=c+d\), то \(a-d=c-b\).

3) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.

4) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.

5) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).

6) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.