стр. 61. Проверьте себя - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Проверьте себя
Вопрос
Проверочная работа
1. Вычислите:
а) 48 : (-3);
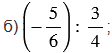
в) |0,39| : |-1,3|;
г) 0 : (-19).
2. Найдите значение выражения:
а) (3 - 13) : (-17 + 7);
б) (-1,2 - 1,2) : (-1 - 2);

3. Решите уравнение:
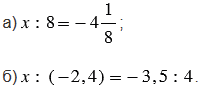
4. Определите знак выражения:
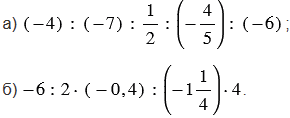
Подсказка
Вспомните:
- Деление положительных и отрицательных чисел.
- Модуль числа.
- Противоположные числа.
- Порядок выполнения действий.
- Сложение положительных и отрицательных чисел.
- Вычитание положительных и отрицательных чисел.
- Умножение положительных и отрицательных чисел.
- Что называют уравнением, его корни.
- Свойство пропорции.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю
- Основное свойство дроби (сокращение дробей).
- Смешанные числа.
- Неправильные дроби.
Ответ


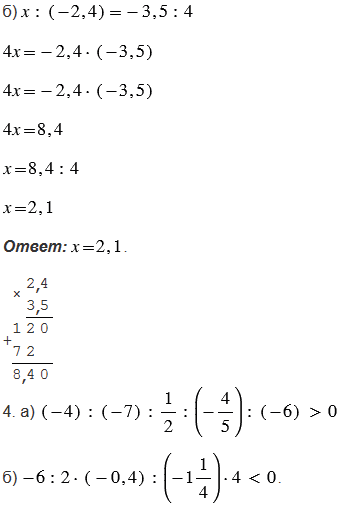
Пояснения:
При выполнении вычислений помним:
1) чтобы сложить два числа с разными знаками, надо: найти модули слагаемых; из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем;
2) чтобы сложить два отрицательных числа, надо: найти модули слагаемых; сложить модули слагаемых; перед полученным числом поставить знак "-";
3) чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому;
4) чтобы перемножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак "-";
5) чтобы перемножить два отрицательных числа, надо перемножить их модули;
6) чтобы найти частное двух отрицательных чисел, надо разделить модуль делимого на модуль делителя;
7) чтобы найти частное двух чисел с разными знаками, надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак "-".
Модуль любого принимает только неотрицательные значения.
Во втором задании порядок выполнения действий определяем по следующему правилу: если в выражении есть скобки (скобки, которые определяют отрицательное число не учитываем), то сначала выполняют действия в скобках, а затем за скобками, при этом как в скобках, так и за скобками, сначала выполняют действия второй ступени (умножение и деление) по порядку слева направо, а потом действия первой ступени (сложение и вычитание), также по прядку слева направо.
В третьем задании в пункте а) помним, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. В пункте б) сначала используем основное свойство пропорции, согласно которому произведение крайних членов пропорции равно произведению ее средних членов, а затем также находим неизвестный множитель.
В четвертом задании учитываем то, что выражение, в котором есть только действия деления и умножения, будет положительным, если в выражении четное количество отрицательных компонентов, и будет отрицательным, если в выражении нечетное количество отрицательных компонентов (четные числа делятся нацело на 2, а нечетные не делятся нацело на 2).
Вернуться к содержанию учебника