Задание Проверочная работа №2. Проверьте себя - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 95

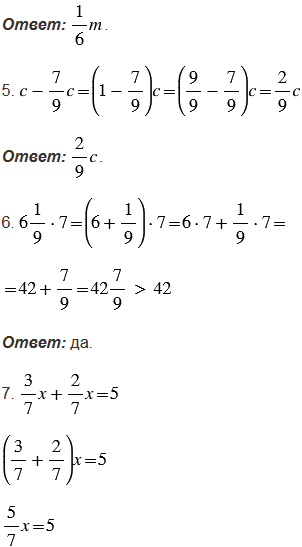
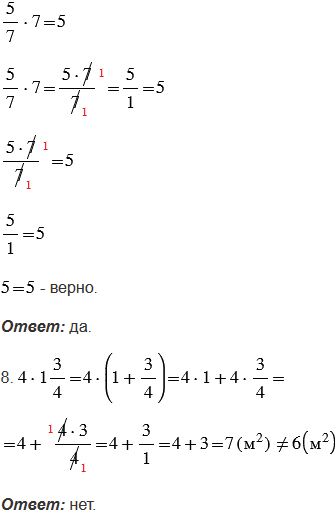
Пояснения:

1. Чтобы умножить сумму на число, используем распределительное свойство умножения относительно сложения, то есть отдельно умножаем каждое слагаемое на число за скобками и складываем полученные результаты. Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. Также помним то, что черту дроби можно заменить делением (числитель делим на знаменатель).

2. Чтобы умножить смешанное число на натуральное число, используем распределительное свойство умножения, а именно, чтобы умножить смешанное число на натуральное число, можно:

1) умножить целую часть на натуральное число;

2) умножить дробную часть на это натуральное число;

3) сложить полученные результаты.

В пунктах 3-5, чтобы упростить выражения, используем распределительное свойство умножения, а именно выносим одинаковый множитель (букву) за скобки и выполняем вычисления в скобках.

3. Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним. Также помним, то что дробь, у которой числитель и знаменатель одинаковые, равны единице.

4. Чтобы вычесть две дроби с разными знаменателями, надо, используя основное свойство дроби, привести данные дроби к общему знаменателю (наименьшее общее кратное знаменателей) и применить правило вычитания дробей с одинаковыми знаменателями: чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

5. При вычислениях учитываем то, что единицу можно представить в виде неправильной дроби, у которой числитель и знаменатель одинаковые.

6. Как умножить смешанное число на натуральное число смотри пункт 2.

7. Чтобы узнать, является ли число корнем уравнения, сначала, используя распределительное свойство умножения, упрощаем левую часть уравнения, а именно выносим одинаковый множитель (букву) за скобки и выполняем вычисления в скобках. Затем число, которое указано как корень уравнения, подставляем в упрощенное уравнение вместо переменной и выполняем вычисления, если равенство получается верным, то число является корнем уравнения.

8. Чтобы найти площадь прямоугольника, нужно перемножить его длину и ширину. Как умножить смешанное число на натуральное число смотри пункт 2.