Задание Проверочная работа. Проверьте себя - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1. Страница 98
Старая и новая редакции
Вернуться к содержанию учебника
Проверьте себя. Страница 98
Проверочная работа №2 Проверочная работа №1 Проверочная работа №2 Проверочная работа Проверочная работа №1 Проверочная работа №2 Проверочная работа №1
Вопрос
№Проверочная работа учебника 2021-2022 (стр. 98):
Запишите число обратное:
1. Одной третьей.
2. Четырем седьмым.
3. Двум целым одной четвертой.
4. Какое число надо умножить на три восьмых, чтобы получить единицу?
5. Каков корень уравнения 0,2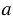 = 1?
= 1?
Верно ли высказывание (ответьте да или нет)?
6. Числа две девятых и три вторых взаимно обратные.
7. Для любого числа существует обратное ему число.
8. Для правильной дроби обратным числом является неправильная дробь.
Подсказка
№Проверочная работа учебника 2021-2022 (стр. 98):
Вспомните:
- Взаимно обратные числа, умножение обыкновенных дробей.
- Что называют уравнением, его корни.
- Правильные и неправильные дроби.
- Десятичная запись дробных чисел.
- Сокращение дробей.
- Деление и дроби.
- Деление с остатком.
Ответ
№Проверочная работа учебника 2021-2022 (стр. 98):
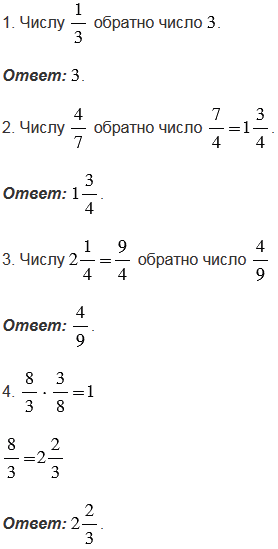

Пояснения:
Произведение двух взаимно обратных чисел равно единице.
Помним:
- Числом, обратным 1, является само число 1.
- Для числа 0 обратного числа не существует.
- Обратным числу
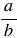 является число
является число 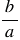 .
. - Если
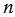 - натуральное число, то обратным ему является число
- натуральное число, то обратным ему является число 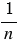 .
.
Чтобы определить число, обратное смешанному числу, нужно преобразовать смешанное число в неправильную дробь и, если возможно, сократить ее. Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Чтобы определить число, обратное десятичной дроби, нужно десятичную дробь преобразовать в обыкновенную дробь, если возможно, сократить ее. У обыкновенной дроби в знаменателе столько нулей, сколько знаков после запятой у десятичной дроби.
Сократить дробь, значит, разделить ее числитель и знаменатель на их наибольший общий делитель.
Если обратное число - неправильная дробь (числитель больше знаменателя), ее нужно преобразовать в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
Правильная дробь - это дробь, у которой числитель меньше знаменателя, обратной этой дроби будет дробь, у которой числитель и знаменатель исходной дроби поменяли местами, то есть это будет дробь, у которой числитель больше знаменатель, а такая дробь является неправильной.
Вернуться к содержанию учебника