Задание 2.422 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.422 учебника 2023-2024 (стр. 101):
Одно число в 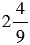 раз больше другого. Найдите эти числа, если их разность равна
раз больше другого. Найдите эти числа, если их разность равна 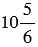 .
.
№2.422 учебника 2021-2022 (стр. 94):
В первый день убрали 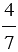 площади, засеянной подсолнечником, во второй день - 0,7 оставшейся площади. Сколько гектаров подсолнечника убрали за эти два дня, если было засеяно
площади, засеянной подсолнечником, во второй день - 0,7 оставшейся площади. Сколько гектаров подсолнечника убрали за эти два дня, если было засеяно 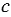 га? Найдите значение получившегося выражения при
га? Найдите значение получившегося выражения при 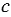 = 35;
= 35; 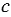 = 42.
= 42.
Подсказка
№2.422 учебника 2023-2024 (стр. 101):
Вспомните:
- Что называют уравнением, его корни.
- Распределительное свойство умножения.
- Деление обыкновенных дробей.
- Умножение обыкновенных дробей, взаимно обратные числа.
- Сокращение дробей.
- Неправильные дроби.
- Деление и дроби.
- Деление с остатком.
- Смешанные числа.
№2.422 учебника 2021-2022 (стр. 94):
Вспомните:
- Как найти дробь от числа, умножение обыкновенных дробей.
- Сокращение дробей.
- Распределительное свойство умножения.
- Числовые и буквенные выражения.
- Сложение и вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Неправильные дроби.
- Деление и дроби.
- Деление с остатком.
- Десятичные дроби.
Ответ
№2.422 учебника 2023-2024 (стр. 101):
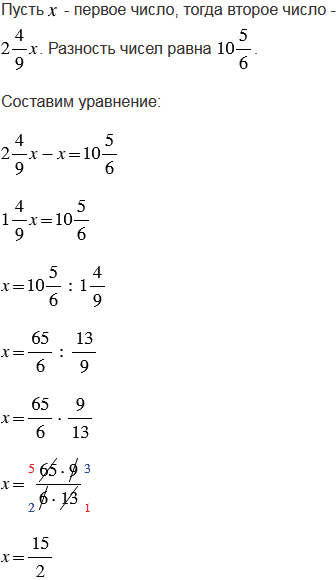


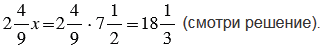
При выполнении вычислений учитываем правила указанные ниже.
Чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 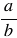 является число
является число 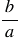 .
.
Чтобы выполнить деление смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Если при вычислениях получилась неправильная дробь (числитель больше знаменателя), преобразуем ее в смешанное число. Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток - как числитель его дробной части.
№2.422 учебника 2021-2022 (стр. 94):






Вернуться к содержанию учебника