Задание 2.425 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.425 учебника 2023-2024 (стр. 101):
Представьте делитель в виде десятичной дроби и найдите частное:
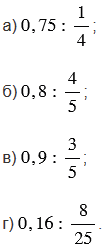
№2.425 учебника 2021-2022 (стр. 96):
Найдите произведение:
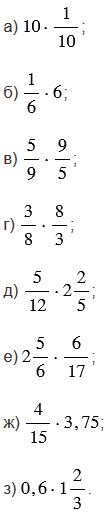
Подсказка
№2.425 учебника 2023-2024 (стр. 101):
Вспомните:
- Десятичную запись дробных чисел
- Основное свойство дроби.
- Деление десятичных дробей.
№2.425 учебника 2021-2022 (стр. 96):
Вспомните:
- Умножение обыкновенных дробей, взаимно обратные числа.
- Смешанные числа.
- Неправильные дроби.
- Десятичные дроби.
- Сокращение дробей.
Ответ
№2.425 учебника 2023-2024 (стр. 101):
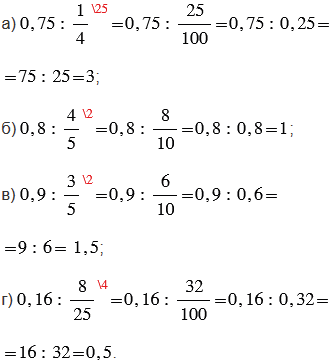
Пояснения:
Чтобы преобразовать обыкновенную дробь в десятичную, используем основное свойство дроби, а именно, умножаем обыкновенную дробь на такой дополнительный множитель, чтобы в знаменателе получилась единица с нулями (10, 100, 1000 и т.д.). Затем полученную обыкновенную дробь записываем в виде десятичной дроби, учитывая то, что количество знаков после запятой у десятичной дроби совпадает с количеством нулей в знаменателе обыкновенной дроби.
Чтобы разделить десятичную дробь на натуральное число, нужно разделить дробь на это число, не обращая внимания на запятую и поставить в частном запятую, когда кончится деление целой части.
№2.425 учебника 2021-2022 (стр. 96):
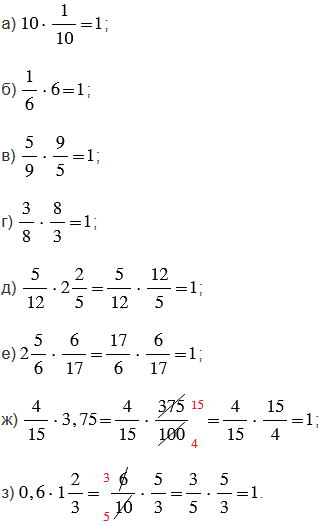
Пояснения:
Произведение двух взаимно обратных чисел равно единице.
Помним:
- Числом, обратным 1, является само число 1.
- Для числа 0 обратного числа не существует.
- Обратным числу
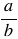 является число
является число 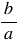 .
. - Если
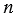 - натуральное число, то обратным ему является число
- натуральное число, то обратным ему является число 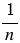 .
.
В пунктах д) - з), чтобы найти произведение, преобразуем смешанные числа в неправильные дроби, и если возможно сокращаем их, а десятичные дроби в обыкновенные дроби и также, если возможно сокращаем их.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
У обыкновенной дроби в знаменателе столько нулей, сколько знаков после запятой у десятичной дроби.
Сократить дробь, значит, разделить ее числитель и знаменатель на их наибольший общий делитель.
Вернуться к содержанию учебника