Страница 55 - ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
Стр. 55 учебника 2023-2025:
3. Начерти и вырежи 2 таких квадрата (1 и 2). Первый квадрат разрежь на части, как показано на рисунке. Из полученных треугольников и квадрата 2 сложи квадрат 3. Найди его площадь.
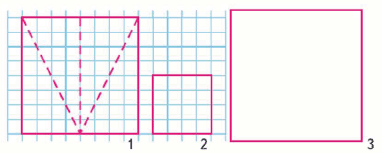
Стр. 55 учебника 2011-2022:
12. Сравни скорости, с которыми могут двигаться разные животные (с. 78-79).
Подсказка
Ответ
Стр. 55 учебника 2023-2025:
Решение
4 • 4 + 2 • 2 = 20 (см2) - площадь квадрата.
Пояснение
Площадь образованного квадрата равна площади квадрата 1 и квадрата 2.
Площадь квадрата можно определить, умножив сторону саму на себя.
Площадь квадрата 1:
4 • 4 (см2).
Площадь квадрата 2:
2 • 2 (см2).
Значит, площадь образованного квадрата:
4 • 4 + 2 • 2 = 16 + 4 = 20 (см2).
Стр. 55 учебника 2011-2022:
Вариант ответа #1:
Список животных от самого медленного к самому быстрому:
страус, аист, жираф, воробей и зебра, лев, голубь и антилопа, гепард, стриж.
Пояснение
Выразим скорости всех рассматриваемых животных в км/ч.
Аист: 600 м/мин = 600 • 60 =
= 36 000 м/мин = 36 км/ч.
Голубь: 90 км/ч.
Воробей: 60 км/ч.
Стриж:
3 км/мин = 3 • 60 км/ч = 180 км/ч.
Гепард: 30 м/с = 30 • 3 600 м/ч =
= 108 000 м/ч = 108 км/ч.
Антилопа: 25 м/с = 25 • 3 600 м/ч =
= 90 000 м/ч = 90 км/ч
| × | 3 | 6 | 0 | 0 | |
| 2 | 5 | ||||
| + | 1 | 8 | 0 | ||
| 7 | 2 | ||||
| 9 | 0 | 0 | 0 | 0 |
Лев: 80 км/ч.
Страус: 500 м/мин = 500 • 60 м/ч =
= 30 000 м/ч = 30 км/ч.
Зебра:
1 км/мин = 1 • 60 км/ч = 60 км/ч.
Жираф: 750 м/мин = 750 • 60 м/ч =
= 45 000 м/ч = 45 км/ч.
| × | 7 | 5 | 0 | |
| 6 | 0 | |||
| 4 | 5 | 0 | 0 | 0 |
Расположим скорости в порядке возрастания (от меньшей к большей):
30 км/ ч < 36 км/ч < 45 км/ч < 60 км/ч <
< 80км/ч < 90км/ч < 108км/ч < 180км/ч.
Тогда список животных от самого медленного к самому быстрому будет выглядеть так:
страус, аист, жираф, воробей и зебра, лев, голубь и антилопа, гепард, стриж.
Вариант ответа #2:
Решение
Скорость гепарда больше скорости антилопы на 5 м/с.
Зебра двигается быстрее жирафа и страуса, но медленнее льва.
Пояснение
Гепард двигается со скоростью 30 м/с, а антилопа со скоростью 25 м/с. Значит, гепард движется быстрее на 30 - 25 = 5 м/с.
Зебра движется со скоростью 1 км/мин, то есть 1000 м/мин, жираф со скоростью 750 м/мин, страус - 500 м/мин, а 1000 > 750 и 500. Лев движется со скоростью 80 км/ч, а 80 > 1.
Вопрос
Выберите год учебника
Стр. 55 учебника 2023-2025:
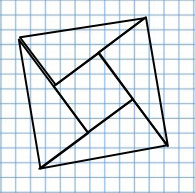
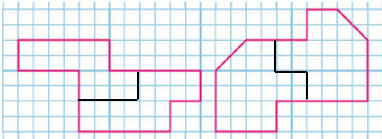
4. Начерти и вырежи такие же фигуры. Разрежь каждую из них на 2 такие части, которые при наложении совпадут.
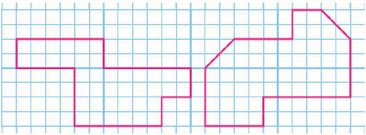
Стр. 55 учебника 2011-2022:
13. 1) Дана сумма 36 + 44. Каждое слагаемое увеличили в 20 раз. Проверь, увеличится ли в 20 раз значение суммы.
2) Дано произведение 15 • 10. Первый множитель увеличили в 4 раза, а второй оставили без изменения. Проверь, увеличится ли в 4 раза значение произведения.
Подсказка
Ответ
Вопрос
Выберите год учебника
Стр. 55 учебника 2023-2025:
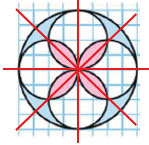
5. Рассмотри чертёж. Начерти такие же узоры. Раскрась один из них. Сколько осей симметрии у первой фигуры?
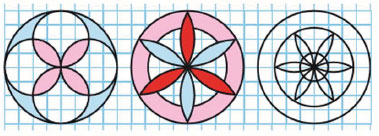
Стр. 55 учебника 2011-2022:
14.
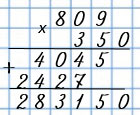
| 986 • 134 | 809 • 350 |
| 701 • 235 | 406 • 502 |
| 34 • (120 - 3 920 : 70) | |
| (110 - 3 420 : 90) • 25 | |
Подсказка
Ответ
Стр. 55 учебника 2023-2025:
Воспользуйтесь циркулем, начертите узоры и раскрасьте один из них.
У первой фигуры 4 оси симметрии.
Пояснение
Ось симметрии фигуры - это прямая, которая делит фигуру на две симметричные части (если по этой прямой перегнуть фигуру, то ее части наложатся друг на друга). Значит, первая фигура имеет 4 оси симметрии.
Стр. 55 учебника 2011-2022:
Решение
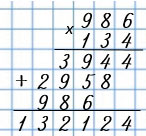 |
 |
 |
 |
34 • (120 - 3 920 : 70) = 2 176
(110 - 3 420 : 90) • 25 = 1 800
Пояснение
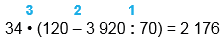
| 1) | - | 3 | 9 | 2 | 0 | 7 | 0 | |||||||||
| 3 | 5 | 0 | 5 | 6 | ||||||||||||
| - | 4 | 2 | 0 | |||||||||||||
| 4 | 2 | 0 | ||||||||||||||
| 0 |
| • | • | |||
| 2) | - | 1 | 2 | 0 |
| 5 | 6 | |||
| 6 | 4 |
| 3) | × | 3 | 4 | ||
| 6 | 4 | ||||
| + | 1 | 3 | 6 | ||
| 2 | 0 | 4 | |||
| 2 | 1 | 7 | 6 |

| 1) | - | 3 | 4 | 2 | 0 | 9 | 0 | |||||||||
| 2 | 7 | 0 | 3 | 8 | ||||||||||||
| - | 7 | 2 | 0 | |||||||||||||
| 7 | 2 | 0 | ||||||||||||||
| 0 |
| • | • | |||
| 2) | - | 1 | 1 | 0 |
| 3 | 8 | |||
| 7 | 2 |
| 3) | × | 7 | 2 | ||
| 2 | 5 | ||||
| + | 3 | 6 | 0 | ||
| 1 | 4 | 4 | |||
| 1 | 8 | 0 | 0 |
Вопрос
15. Выполни деление с остатком.
448 : 10
683 : 10
367 : 80
421 : 50
293 : 70
Подсказка
Повтори алгоритм деления с остатком.
Ответ
Решение
 |
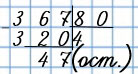 |
 |
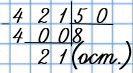 |
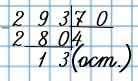 |
|
Пояснение
Первое неполное делимое - 44 десятка. В записи частного будет 2 цифры.
Разделю 44 на 10. Для этого разделю 4 на 1, получу 4 - столько десятков будет в частном.
Умножу 10 на 4, получу 40 - столько десятков разделили.
Вычту 40 из 44, получу 4 - столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 10.
Второе неполное делимое - 48 единиц.
Разделю 48 на 10. Для этого разделю 4 на 1, получу 4 - столько единиц будет в частном.
Умножу 10 на 4, получу 40 - столько единиц разделили.
Вычту 40 из 48, получу 8 - столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 40.
Читаю ответ: частное равно 44, остаток 8.
Далее рассуждаю аналогично.
Вопрос
16. Составь и реши задачи по рисункам животных (с. 79).
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Вариант ответа #1:
1) Гепард и Антилопа бегут навстречу друг другу. Гепард бежит со скоростью 30 м/с, а антилопа - 25 м/с. Через 60 с гепард заметил антилопу на расстоянии 100 м от него. Какое расстояние было между гепардом и антилопой изначально?
1) 30 + 25 = 55 (м/с) - скорость сближения.
2) 55 • 60 = 3 300 (м) - расстояние, которое пробежали гепард и антилопа вместе.
| × | 5 | 5 | |
| 6 | 0 | ||
| 3 | 3 | 0 | 0 |
3) 3 300 + 100 = 3 400 (м)
Ответ: между гепардом и антилопой изначально было 3 400 м.
2) Лев бежит со скоростью 80 км/ч, а зебра - 1 км/мин. Кто пробежит быстрее и на сколько расстояние, равное 240 км?
1 км/мин = 1 • 60 км/ч = 60 км/ч.
1) 240 : 80 = 3 (ч) - время, которое бежит лев.
2) 240 : 60 = 4 (ч) - время, которое бежит зебра.
3) 4 - 3 = 1 (ч)
Ответ: лев пробежит быстрее, чем зебра, на 1 ч.
3) Страус и жираф участвовали в эстафете. Страус бежал первые 4 мин со скоростью 500 м/мин, а жираф следующие 3 мин со скоростью 750 м/мин. Какое общее расстояние пробежали страус и жираф?
1) 500 • 4 = 2 000 (м) - пробежал страус.
2) 750 • 3 = 2 250 (м) - пробежал жираф.
| × | 7 | 5 | 0 |
| 3 | |||
| 2 | 2 | 5 | 0 |
3) 2 000 + 2 250 = 4 250 (м)
Ответ: страус и жираф пробежали 4 250 м.
Пояснение
Чтобы найти расстояние, нужно скорость умножить на время.
Чтобы найти время, нужно расстояние разделить на скорость.
Вариант ответа #2:
Решение
Гепард бегает со скоростью 30 м/с, а антилопа - 25 м/с. На сколько больше метров пробежит гепард, чем антилопа, за 3 мин?
1) 30 • 3 = 90 (м) - гепард за 3 мин.
2) 25 • 3 = 75 (м) - антилопа за 3 мин.
3) 90 - 75 = 15 (м)
Ответ: на 15 м больше пробежит гепард.
Скорость страуса - 500 м/мин, а скорость жирафа - 750 м/мин. На сколько выше скорость жирафа?
750 - 500 = 250 (м/мин)
Ответ: на 250 м/мин выше скорость жирафа.
Пояснение
Задача 1:
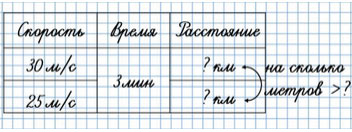
Сколько метров пробежит гепард за 3 мин?
1) 30 • 3 = 90 (м)
Сколько метров пробежит антилопа за 3 мин?
2) 25 • 3 = 75 (м)
На сколько больше метров пробежит гепард, чем антилопа, за 3 мин?
3) 90 - 75 = 15 (м)
Скорость гепарда - 30 м/мин, вычислим, сколько он пробежит за 3 минуты:
1) 30 • 3 = 90 (м)
Скорость антилопы - 25 м/мин, вычислим, сколько она пробежит за 3 минуты:
2) 25 • 3 = 75 (м)
Гепард пробежит за 3 минуты - 90 м, а антилопа - 75 м. Узнаем, на сколько больше метров пробежит гепард, чем антилопа, за 3 минуты:
3) 90 - 75 = 15 (м)
Задача 2:
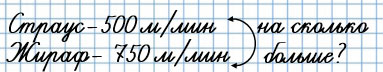
Вопрос
17. Реши задачи и сравни их решения.
1) В один магазин привезли 18 одинаковых бидонов молока, а в другой - 12 таких же бидонов. В первый магазин привезли на 228 л молока больше, чем во второй. Сколько литров молока привезли в каждый магазин?
2) В один магазин привезли в одинаковых бидонах 684 л молока, а в другой - 456 л молока в таких же бидонах. В первый магазин привезли на 6 бидонов молока больше, чем во второй. Сколько бидонов молока привезли в каждый магазин?
Подсказка
Повтори единицу объёма - литр.
Ответ
Решение
Задача 1:
1) 18 - 12 = 6 (б.) - на столько больше.
2) 228 : 6 = 38 (л) - в одном бидоне.
| - | 2 | 2 | 8 | 6 | ||||||||||
| 1 | 8 | 3 | 8 | |||||||||||
| - | 4 | 8 | ||||||||||||
| 4 | 8 | |||||||||||||
| 0 |
3) 38 • 18 = 684 (л) - в одном магазине.
| × | 3 | 8 |
| 1 | 8 | |
| 3 | 0 | 4 |
| 3 | 8 | |
| 6 | 8 | 4 |
4) 38 • 12 = 456 (л) - в другом магазине.
| × | 3 | 8 |
| 1 | 2 | |
| 7 | 6 | |
| 3 | 8 | |
| 4 | 5 | 6 |
Ответ: 684 л, 456 л.
Задача 2:
1) 684 - 456 = 228 (л) - на столько больше.
| • | |||
| - | 6 | 8 | 4 |
| 4 | 5 | 6 | |
| 2 | 2 | 8 |
2) 228 : 6 = 38 (л) - в одном бидоне.
| - | 2 | 2 | 8 | 6 | ||||||||||
| 1 | 8 | 3 | 8 | |||||||||||
| - | 4 | 8 | ||||||||||||
| 4 | 8 | |||||||||||||
| 0 |
3) 684 : 38 = 18 (б.) - в один магазин.
| - | 6 | 8 | 4 | 3 | 8 | |||||||||
| 3 | 8 | 1 | 8 | |||||||||||
| - | 3 | 0 | 4 | |||||||||||
| 3 | 0 | 4 | ||||||||||||
| 0 |
4) 456 : 38 = 12 (б.) - в другой магазин.
| - | 4 | 5 | 6 | 3 | 8 | |||||||||
| 3 | 8 | 1 | 2 | |||||||||||
| - | 7 | 6 | ||||||||||||
| 7 | 6 | |||||||||||||
| 0 |
Ответ: 18 бидонов, 12 бидонов.
Это обратные задачи.
Пояснение
Задача 1:
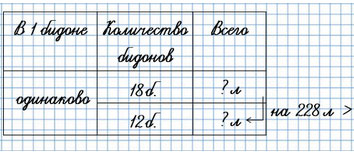
На сколько больше привезли бидонов в один магазин, чем в другой магазин?
1) 18 - 12 = 6 (б.)
Сколько литров молока в одном бидоне?
2) 228 : 6 = 38 (л)
Сколько литров молока привезли в один магазин?
3) 38 • 18 = 684 (л)
Сколько литров молока привезли в другой магазин?
4) 38 • 12 = 456 (л)
В один магазин привезли 18 одинаковых бидонов, а в другой - 12 таких же бидонов. Вычислим, на сколько больше бидонов привезли в первый магазин:
1) 18 - 12 = 6 (б.)
В первый магазин привезли на 6 бидонов больше, в которых было 228 л молока. Вычислим, сколько литров молока в одном бидоне:
2) 228 : 6 = 38 (л)
В одном бидоне 38 л молока. В первый магазин привезли 18 таких бидонов. Узнаем, сколько литров молока привезли в первый магазин:
3) 38 • 18 = 684 (л)
В одном бидоне 38 л молока. Во второй магазин привезли 12 таких бидонов. Узнаем, сколько литров молока привезли в другой магазин:
4) 38 • 12 = 456 (л)
Задача 2:

На сколько больше литров молока привезли в первый магазин, чем во второй?
1) 684 - 456 = 228 (л)
Сколько литров молока в одном бидоне?
2) 228 : 6 = 38 (л)
Сколько бидонов молока привезли в первый магазин?
3) 684 : 38 = 18 (б.)
Сколько бидонов молока привезли во второй магазин?
4) 456 : 38 = 12 (б.)
В один магазин привезли 684 л молока, а в другой - 456 л молока. Вычислим, на сколько больше литров молока привезли в первый магазин:
1) 684 - 456 = 228 (л)
В первый магазин привезли на 6 бидонов больше, в которых было 228 л молока. Вычислим, сколько литров молока в одном бидоне:
2) 228 : 6 = 38 (л)
В один магазин привезли 684 л молока, по 38 л в каждом бидоне. Узнаем, сколько бидонов молока привезли в первый магазин:
3) 684 : 38 = 18 (б.)
Во второй магазин привезли 456 л молока, по 38 л в каждом бидоне. Узнаем, сколько бидонов молока привезли в другой магазин:
4) 456 : 38 = 12 (б.)
Вопрос
18. Реши уравнения.
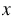 - 12 = 0 - 12 = 0 |
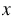 : 108 = 1 : 108 = 1 |
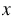 • 15 = 0 • 15 = 0 |
25 + 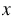 = 25 = 25 |
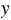 : 1 = 37 : 1 = 37 |
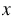 • 18 = 18 • 18 = 18 |
Подсказка
Повтори, как решать уравнения.
Ответ
Решение
|
|
|
|
|
25 +
|
|
|
Пояснение
1. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность:
12 + 0 = 12.
Проверка:
12 - 12 = 0
0 = 0
2. Чтобы найти второе слагаемое, нужно из суммы вычесть первое слагаемое:
25 - 25 = 0.
Проверка:
25 + 0 = 25.
25 = 25
3. Чтобы найти делимое, нужно частное умножить на делитель:
108 • 1 = 108.
Проверка:
108 : 108 = 1
1 = 1
4. Чтобы найти делимое, нужно частное умножить на делитель:
37 • 1 = 37.
Проверка:
37 : 1 = 37
37 = 37
5. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
0 : 15 = 0.
Проверка:
0 • 15 = 0
0 = 0
6. Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
18 : 18 = 1.
Проверка:
1 • 18 = 18
18 = 18
Вопрос
19. Начерти и вырежи 4 квадрата со стороной 4 см. Составь из них 2 разных прямоугольника и найди периметр и площадь каждого из них.
Подсказка
Повтори, какие бывают многоугольники, а также как найти периметр и площадь прямоугольника.
Ответ
Решение
1)
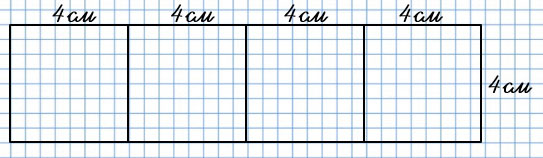
(4 • 4) • 4 = 64 (см2) - площадь прямоугольника.
(4 • 4 + 4) • 2 = 40 (см) - периметр прямоугольника.
2)
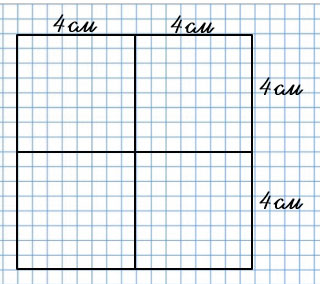
(4 • 2) • (4 • 2) = 64 (см2) - площадь прямоугольника.
(4 • 2) • 4 = 32 (см) - периметр прямоугольника.
Пояснение
Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину. У 1 прямоугольника длина состоит из 4 отрезков по 4 см, значит длина (4 • 4) см, а ширина 4 см.
У 2 прямоугольника длина состоит из 2 отрезков по 4 см, значит длина (4 • 2) см. Так как этот прямоугольник является квадратом, то ширина тоже - (4 • 2) см.
Чтобы найти периметр прямоугольника, нужно найти сумму длин всех его сторон. Мы знаем, что противоположные стороны прямоугольника равны. Поэтому можно сумму длины и ширины умножить на 2. У 1 прямоугольника длина состоит из 4 отрезков по 4 см, значит длина (4 • 4) см, а ширина 4 см.
У 2 прямоугольника длина состоит из 2 отрезков по 4 см, значит длина (4 • 2) см. Так как этот прямоугольник - квадрат, то его периметр равен произведению длины любой его стороны на четыре (так как всего его стороны равны).
Вопрос
20. Рассмотри чертёж и выпиши названия всех треугольников с общей стороной АС; ВС.
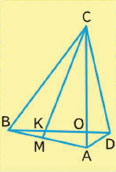
Подсказка
Повтори, какие бывают треугольники.
Вопрос
21. 1) Объясни, почему на 2 делится без остатка любое число, в записи которого последняя цифра 0, 2, 4, 6 или 8.
2) Какой должна быть последняя цифра в записи числа, которое делится без остатка на 5?
Подсказка
Повтори, что такое деление с остатком.
Ответ
Решение
1) Любое число, которое оканчивается на 0, 2, 4, 6 или 8 является чётным. Если поделить чётное число на 2, то оно будет делится без остатка.
2) Чтобы число делилось на 5 без остатка, последняя цифра в записи числа должна быть 0 или 5.
Пояснение
Четным числом называется целое число, которое делится на 2 без остатка.
Вопрос
Найди лишнее выражение

Ответ
Вернуться к содержанию учебника
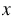 - 12 = 0
- 12 = 0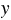 : 1 = 37
: 1 = 37