Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

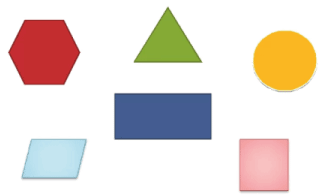
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Например, площадь в городе  - это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь - это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник : 

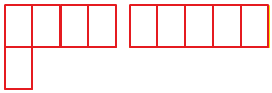
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками. 

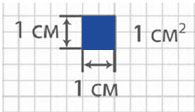
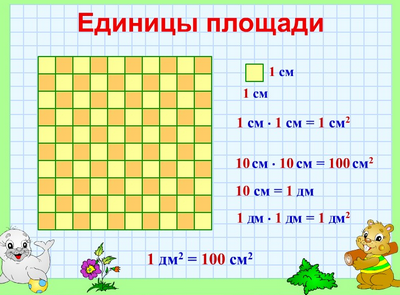
Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

Определим площадь данных фигур:

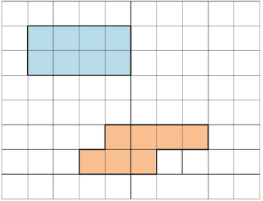
В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

1 дм² = ? см²

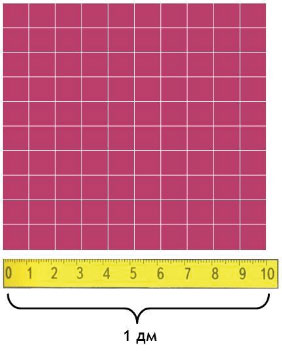
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

10  • 10 = 100 см²

Значит, 1 дм² = 100 см²

Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

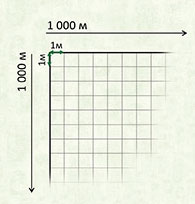
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

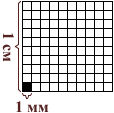
Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

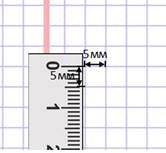
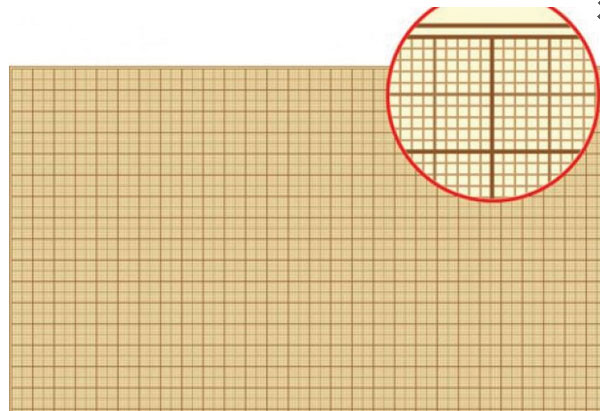
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Ар - это площадь квадрата со стороной 10 м.

Слово "ар" при числах сокращённо записывают так:

1 а, 20 а, 97 а.

1 а² = 100 м², поэтому ар часто называют соткой.

Гектар

Гектар - это площадь квадрата со стороной 100 м.

Слово "гектар" при числах сокращённо записывают так:

1 га, 20 га, 530 га.

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.