Страница 92 - ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
12. Дима купил для украшения ёлки 4 игрушки по одинаковой цене, а Настя - 3 такие же игрушки. Все эти игрушки стоили 56 р.
Объясни, что обозначают выражения.
3 + 4
56 : (3 + 4)
56 : (3 + 4) • 3
56 : (3 + 4) • 4
Подсказка
Повтори, что такое числовые выражения.
Ответ
Решение
3 + 4 - количество игрушек.
56 : (3 + 4) - цена одной игрушки.
56 : (3 + 4) • 3 - стоимость игрушек Насти.
56 : (3 + 4) • 4 - стоимость игрушек Димы.
Пояснение
3 + 4 - общее количество игрушек.
Количество игрушек - (3 + 4), а стоимость 56 р. Чтобы найти цену, нужно стоимость разделить на количество:
56 : (3 + 4).
Чтобы найти стоимость, нужно цену умножить на количество. Узнаем стоимость игрушек Насти:
56 : (3 + 4) • 3
Узнаем стоимость игрушек Димы:
56 : (3 + 4) • 4
Вопрос
13. Мальчик купил 6 тетрадей в клетку и 5 тетрадей в линейку по одинаковой цене. Всего он заплатил d р. Объясни, что обозначают выражения.
| 6 + 5 | d : (6 + 5) | d : (6 + 5) • 6 |
Подсказка
Повтори, что такое буквенные выражения.
Ответ
Решение
6 + 5 - количество купленных тетрадей.
d : (6 + 5) - цена одной тетради.
d : (6 + 5) • 6 - стоимость тетрадей в клетку.
Пояснение
6 + 5 - общее количество тетрадей.
Стоимость игрушек - d р., а количество - (6 + 5). Чтобы узнать цену одной тетради, нужно стоимость разделить на количество:
d : (6 + 5).
Чтобы найти стоимость, нужно цену умножить на количество. Узнаем стоимость тетрадей в клетку:
d : (6 + 5) • 6.
Вопрос
14. В одном куске 5 м ткани, в другом куске 7 м такой же ткани. За оба куска заплатил d р. За оба куска заплатили k р. Объясни, что обозначают выражения.
k : (5 + 7)
k : (5 + 7) • 5
k : (5 + 7) • 7
Подсказка
Повтори, что такое буквенные выражения.
Ответ
Решение
k : (5 + 7) - цена 1 м ткани.
k : (5 + 7) • 5 - цена одного куска ткани.
k : (5 + 7) • 7 - цена другого куска ткани.
Пояснение
5 + 7 - общее количество метров ткани. Их стоимость - р. Чтобы узнать цену 1 м ткани, нужно стоимость разделить на количество:
k : (5 + 7).
Чтобы узнать стоимость, нужно цену умножить на количество. Вычислим стоимость одного куска:
k : (5 + 7) • 5.
Вычислим стоимость другого куска:
k : (5 + 7) • 7.
Вопрос
Выберите год учебника
Стр. 92 учебника 2023-2025:
15. Как можно, не изменяя чисел, сделать равенства верными? Выполни это.
78 - 60 : 2 + 4 = 13
78 - 60 : 2 + 4 = 44
Стр. 92 учебника 2011-2022:
15. Расставь скобки так, чтобы равенства стали верными.
78 - 60 : 2 + 4 = 13
78 - 60 : 2 + 4 = 44
Подсказка
Повтори, как выполнять действия со скобками.
Ответ
Вопрос
16. Во сколько раз 1 дм больше, чем 1 мм? 1 ц больше, чем 10 кг? 1 ч больше, чем 10 мин? 1 км больше, чем 100 м? 1 м2 больше, чем 1 см2?
Подсказка
Ответ
Решение
1 дм больше, чем 1 мм, в 100 раз.
1 ц больше, чем 10 кг, в 10 раз.
1 ч больше, чем 10 мин, в 6 раз.
1 км больше, чем 100 м, в 10 раз.
1 м2 больше, чем 1 см2, в 10000 см2.
Пояснение
Чтобы узнать во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.
1 дм = 100 мм
1 ц = 100 кг, значит, 1 ц больше, чем 10 кг, в 100 : 10 = 10 раз.
1 ч = 60 мин, значит, 1 ч больше, чем 10 мин, в 60 : 10 = 6 раз.
1 км = 1000 м, значит, 1 км больше, чем 100 м, в 1000 : 100 = 10 раз.
1 м2 = 10000 см2
Вопрос
17. Спортсмен прыгнул в высоту на 2 м 35 см, это на 49 см выше его роста. Какого роста был этот спортсмен?
Ответ
Вопрос
18. Хлебозавод ежедневно выпекал одинаковое количество хлеба. За 3 дня было выпечено 705 т хлеба. Сколько хлеба было выпечено за неделю?
Подсказка
Ответ
Решение
1) 705 : 3 = 235 (т) - за 1 день.
| - | 7 | 0 | 5 | 3 | |||||||||||
| 6 | 2 | 3 | 5 | ||||||||||||
| - | 1 | 0 | |||||||||||||
| 9 | |||||||||||||||
| - | 1 | 5 | |||||||||||||
| 1 | 5 | ||||||||||||||
| 0 |
2) 235 • 7 = 1 645 (т)
| × | 2 | 3 | 5 | |
| 7 | ||||
| 1 | 6 | 4 | 5 |
Ответ: 1 645 т хлеба было выпечено за неделю.
Пояснение

Сколько тонн хлеба было выпечено за 1 день?
1) 705 : 3 = 235 (т)
Сколько тонн хлеба было выпечено за неделю?
2) 235 • 7 = 1 645 (т)
За 3 дня было выпечено 705 т хлеба. Вычислим, сколько тонн хлеба было выпечено за 1 день:
1) 705 : 3 = 235 (т)
За 1 день выпекали 235 т хлеба. Узнаем, сколько тонн хлеба было выпечено за неделю:
2) 235 • 7 = 1 645 (т)
Вопрос
19. За 3 ч езды на легковой машине израсходовали 27 л бензина. На сколько часов езды хватит 96 л бензина, если расход его уменьшится на 1 л в час.
Подсказка
Ответ
Решение
1) 27 : 3 = 9 (л) - за 1 час было.
2) 9 - 1 = 8 (л) - за 1 час стало.
3) 96 : 8 = 12 (ч)
Ответ: на 12 ч хватит 96 л бензина.
Пояснение
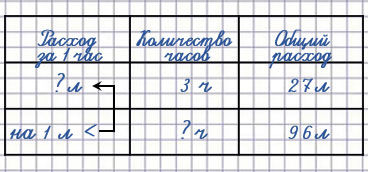
Сколько литров бензина расходовали за 1 час?
1) 27 : 3 = 9 (л)
Сколько литров бензина стали расходовать за 1 час?
2) 9 - 1 = 8 (л)
На сколько часов езды хватит 96 л бензина?
3) 96 : 8 = 12 (ч)
За 3 часа езды израсходовали 27 л бензина. Вычислим, сколько литров бензина тратит машина за 1 ч:
1) 27 : 3 = 9 (л)
Машина расходовала 9 л бензина за 1 ч, теперь расход уменьшился на 1 л. Вычислим, сколько литров бензина стала тратить машина за 1 ч:
2) 9 - 1 = 8 (л)
За 1 ч машина тратит 8 л бензина. Узнаем, на сколько часов езды хватит 96 л бензина:
3) 96 : 8 = 12 (ч)
Вопрос
20. Вычисли результат и выполни проверку.
| 3 509 + 45 845 | 7 306 • 4 |
| 50 102 - 6 945 | 87 540 : 6 |
Ответ
Решение
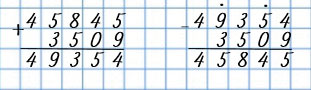 |
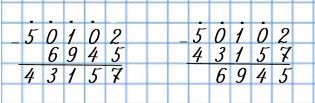 |
 |
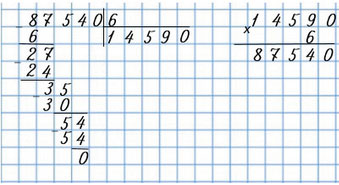 |
Пояснение
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч): 45 845 + 3 509.
Складываю единицы: 5 + 9 = 14. 14 ед. - это 1 дес. и 4 ед.; 4 ед. пишу под единицами, а 1 дес. прибавлю к десяткам.
Складываю десятки: 4 + 0 = 4, да ещё 1.
4 + 1 = 5. Пишу 5 под десятками.
Складываю сотни: 8 + 5 = 13.
13 сот. - это 1 ед. тыс. и 3 сот.; 3 сот. пишу под сотнями, а 1 ед. тыс. прибавлю к ед. тыс.
Складываю единицы тысяч: 5 + 3 = 8, да ещё 1. 8 + 1 = 9. Пишу 9 под единицами тысяч.
Пишу 4 под десятками тысяч, так как других десятков тысяч для сложения нет.
Читаю ответ: 49 354.
Чтобы проверить сложение, можно из суммы вычесть одно из слагаемых и в результате вычислений должно получиться другое слагаемое.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 50 102 - 6 945.
Вычитаю единицы: из 2 ед. нельзя вычесть 5 ед. Взять 1 дес. из 0 дес. нельзя, поэтому беру 1 сот. из 1 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 1.) 1 сот. - это 10 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 0.) 1 дес. и 2 ед. - это 12 ед. Из 12 вычесть 5, получится 7. Пишу под единицами 7.
Вычитаю десятки: было 10 дес., но 1 дес. взяли при вычитании единиц, осталось 9 дес. Из 9 вычесть 4, получится 5. Пишу под десятками 5.
Вычитаю сотни: была 1 сот., но 1 сот. взяли при вычитании единиц, осталось 0 сот. Из 0 сот. нельзя вычесть 9 сот. Взять 1 ед. тыс. из 0 нельзя, поэтому беру 1 дес. тыс. из 5 дес. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 5). 1 дес. тыс. - это 10 ед. тыс. Из 10 ед. тыс. беру 1 ед. тыс. (Чтобы не забыть об этом, ставлю точку над цифрой 0). 1 ед. тыс. и 0 сот. - это 10 сот. Из 10 вычесть 9, получится 1. Пишу под сотнями 1.
Вычитаю единицы тысяч: было 10 ед. тыс., но 1 ед. тыс. взяли при вычитании сотен, осталось 9 ед. тыс. Из 9 вычесть 6, получится 3. Пишу 3 под единицами тысяч.
Вычитаю десятки тысяч: было 5 дес. тыс., но 1 дес. тыс. взяли при вычитании сотен, осталось 4 дес. тыс. Пишу 4 под дес. тыс., так как разряд десятков тысяч в вычитаемом отсутствует.
Читаю ответ: 43 157.
Чтобы проверить вычитание, можно к разности прибавить вычитаемое и в результате вычислений должно получиться уменьшаемое.
Пишу: 7 306 • 4.
Умножаю единицы: 6 • 4 = 24. 24 ед. - это 2 дес. и 4 ед., 4 ед. пишу под единицами, а 2 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 0 • 4 = 0. К 0 дес. прибавляю 2 дес., которые получены при умножении единиц: 0 + 2 = 2. Пишу 2 под десятками.
Умножаю сотни: 3 • 4 = 12. 12 сот. - это 1 ед. тыс. и 2 сот.; 2 сот. пишу под сотнями, а 1 ед. тыс. запомню и прибавлю к единицам тысяч после умножения единиц тысяч.
Умножаю единицы тысяч: 7 • 4 = 28. К 28 ед. тыс. прибавляю 1 ед. тыс, которые получены при умножении сотен: 28 + 1 = 29. 29 ед. тыс. - это 2 дес. тыс. и 9 ед. тыс.; 9 ед. тыс. пишу под единицами тысяч, а 2 дес. тыс. запишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 29 224.
Чтобы проверить умножение, можно произведение разделить на один из множителей и в результате вычислений должен получиться другой множитель.
Пишу: 87 540 : 6.
Делю единицы тысяч.
8 дес. тыс. - это первое неполное делимое, значит в записи частного будет 5 цифр.
Разделю 8 на 6, получу 1 - столько десятков тысяч будет в частном.
Умножу 1 на 6, получу 6 - столько десятков тысяч разделили.
Вычту 6 из 8, получу 2 - столько десятков тысяч осталось разделить.
Сравню остаток с делителем: число оставшихся тысяч меньше, чем 6.
Делю единицы тысяч.
2 дес. тыс. 7 ед. тыс. - всего 27 ед. тыс. Это второе неполное делимое.
Разделю 27 на 6, получу 4 - столько единиц тысяч будет в частном.
Умножу 4 на 6, получу 24 - столько единиц тысяч разделили.
Вычту 24 из 27, получу 3 - столько единиц тысяч осталось разделить.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 6.
Делю сотни.
3 ед. тыс. 5 сот. - всего 35 сот. Это третье неполное делимое.
Разделю 35 на 6, получу 5 - столько сотен будет в частном.
Умножу 5 на 6, получу 30 - столько сотен разделили.
Вычту 30 из 35, получу 5 - столько сотен осталось разделить.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 6.
Делю десятки.
5 сот. 4 дес. - всего 54 дес. Это четвёртое неполное делимое.
Разделю 54 на 6, получу 9 - столько десятков будет в частном.
Умножу 9 на 6, получу 54 - столько десятков разделили.
Вычту 54 из 54, получу 0 - десятки разделили все.
0 ед. нельзя разделить так, чтобы в частном получились единицы.
Читаю ответ: 14 590.
Чтобы проверить деление, можно частное умножить на делитель и в результате вычислений должно получиться делимое.
Вопрос
21. Реши уравнения.
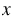 : 9 = 11 : 9 = 11 |
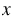 - 80 = 360 - 80 = 360 |
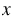 + 75 = 2 075 + 75 = 2 075 |
56 : 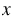 = 56 = 56 |
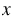 • 8 = 720 • 8 = 720 |
90 - 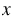 = 90 = 90 |
Подсказка
Повтори, как решать уравнения.
Ответ
Решение
| 1 столбик | |
|
|
|
| 2 столбик | |
|
|
|
| 3 столбик | |
|
56 :
|
90 -
|
Пояснение
Чтобы найти делимое, нужно частное умножить на делитель:
11 • 9 = 99.
Проверка:
99 : 9 = 11
11 = 11
Чтобы найти первое слагаемое, нужно из суммы вычесть второе слагаемое:
2 075 - 75 = 2 000.
Проверка:
2 000 + 75 = 2 075
2 075 = 2 075
Чтобы найти первый множитель, нужно произведение разделить на второй множитель:
720 : 8 = 90.
Проверка:
90 • 8 = 720
720 = 720
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое:
360 + 80 = 440.
Проверка:
440 - 80 = 360
360 = 360
Чтобы найти делитель, нужно делимое разделить на частное:
56 : 56 = 1.
Проверка:
56 : 1 = 56
56 = 56
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность:
90 - 90 = 0.
Проверка:
90 - 0 = 90
90 = 90
Вопрос
22. Найди значение выражения c - k, если c - наименьшее семизначное число, k - наибольшее шестизначное число.
Подсказка
Повтори состав многозначное число.
Ответ
Решение
Если с = 1 000 000, k = 999 999, то
с - k = 1 000 000 - 999 999 = 1
Пояснение
Наименьшее семизначное число - 1 000 000.
Наибольшее шестизначное число - 999 999.
Чтобы найти значение буквенного выражения, нужно в это выражение вместо букв подставить соответствующие числа и выполнить вычисления.
Вернуться к содержанию учебника
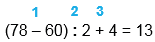
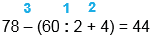
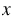 : 9 = 11
: 9 = 11