Конус
Конус - это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.
Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.
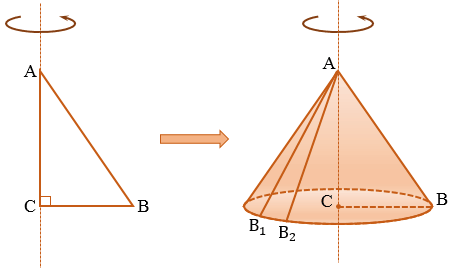
Прямая АС - ось косинуса.
Отрезок АС - высота конуса.
Основание конуса - круг, образованный при вращении катета ВС.
Коническая поверхность (или боковая поверхность конуса) - поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.
Образующие конуса - отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ1 и АВ2).
Определение
| Конус - это тело, ограниченное кругом и конической поверхностью. |
Объем конуса
| Объем конуса равен одной трети произведения площади основания на высоту. |
Доказательство
Дано: конус с площадью основания S, высотой h и объемом V.
Доказать: V = 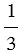 Sh.
Sh.
Доказательство:
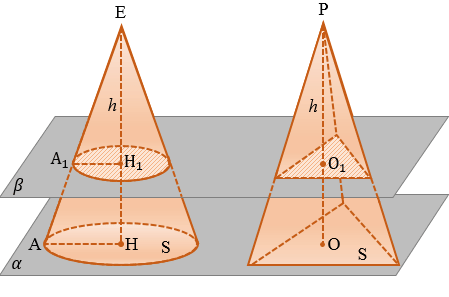
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, "стоящие" на одной плоскости  .
.
Проведем секущую плоскость 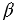 , параллельную плоскости
, параллельную плоскости  и пересекающую высоты ЕН и РО в точках Н1 и О1 соответственно. В сечении конуса плоскостью
и пересекающую высоты ЕН и РО в точках Н1 и О1 соответственно. В сечении конуса плоскостью 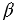 получится круг радиуса Н1А1.
получится круг радиуса Н1А1.
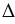 ЕН1А1 подобен
ЕН1А1 подобен 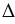 ЕНА по двум углам (
ЕНА по двум углам (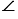 Е - общий,
Е - общий, 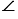 ЕН1А1 =
ЕН1А1 = 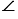 ЕНА = 900, т.к. в противном случае прямые НА и Н1А1, а значит, и плоскости
ЕНА = 900, т.к. в противном случае прямые НА и Н1А1, а значит, и плоскости  и
и 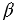 пересекались бы, что противоречит условию). Поэтому
пересекались бы, что противоречит условию). Поэтому 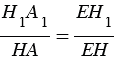 , откуда
, откуда 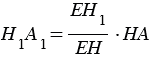 и площадь сечения конуса равна
и площадь сечения конуса равна 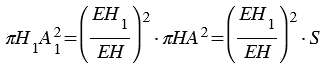 .
.
Площадь сечения пирамиды равна 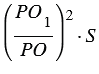 . По условию ЕН = РО = h, значит, ЕН1 = РО1 (т.к. ЕН1 = h - НН1 и РО1 = h - ОО1, параллельные плоскости отсекают одинаковые отрезки НН1 и ОО1 от отрезков ЕН и РО, т.е. НН1 = ОО1).
. По условию ЕН = РО = h, значит, ЕН1 = РО1 (т.к. ЕН1 = h - НН1 и РО1 = h - ОО1, параллельные плоскости отсекают одинаковые отрезки НН1 и ОО1 от отрезков ЕН и РО, т.е. НН1 = ОО1).
Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 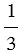 Sh. Что и требовалось доказать.
Sh. Что и требовалось доказать.
Площадь боковой поверхности конуса
Рассмотрим конус с радиусом основания 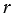 и образующей
и образующей 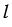 .
.
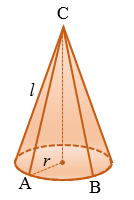
Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.
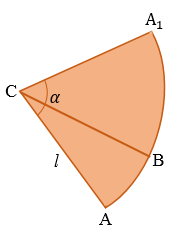
Радиус этого сектора равен образующей конуса, т.е. равен 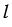 , а длина дуги сектора равна длине окружности основания конуса, т.е. равна 2
, а длина дуги сектора равна длине окружности основания конуса, т.е. равна 2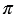
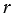 ,
,  - градусная мера дуги сектора, тогда площадь данного сектора:
- градусная мера дуги сектора, тогда площадь данного сектора: 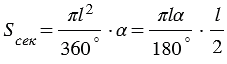 . (1)
. (1)
Длина дуги окружности с градусной мерой  и радиусом
и радиусом 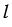 равна
равна 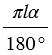 . С другой стороны, длина этой дуги равна 2
. С другой стороны, длина этой дуги равна 2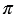
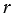 , поэтому учитывая (1), получим:
, поэтому учитывая (1), получим: 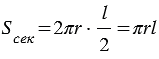 .
.
Площадь боковой поверхности конуса равна площади ее развертки, т.е. 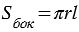 . . |
Советуем посмотреть:
Параллельность и перпендикулярность прямых и плоскостей в пространстве
Свойства прямоугольного параллелепипеда
Правило встречается в следующих упражнениях:
7 класс
Задание 1220, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1221, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1223, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1224, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1249, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1250, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1310, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник