Свойства прямоугольного параллелепипеда
Измерениями прямоугольного параллелепипеда называются длины трёх рёбер с общей вершиной. Например, в качестве измерений у прямоугольного параллелепипеда ABCDA1B1C1D1 можно взять длины рёбер D1D, D1C1 и D1A1, которые имеют общую вершину D1.
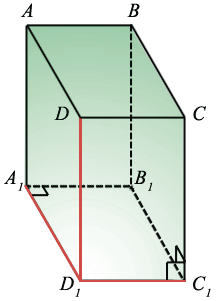
У прямоугольника два измерения - длина и ширина. При этом квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (данное утверждение основывается на теореме Пифагора).
Свойство
| Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. |
Доказательство
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, В1В, В1С1, В1А1 - измерения
Доказать: BD12 = В1В2 + В1С12 + В1А12
Доказательство:
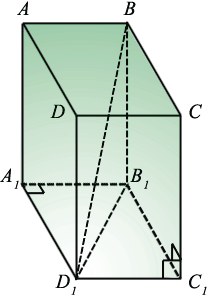
ВВ1 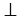 A1B1C1D1, т.е. данное ребро перпендикулярно любой прямой, которая принадлежит плоскости этой грани и проходит через точку В1. Следовательно,
A1B1C1D1, т.е. данное ребро перпендикулярно любой прямой, которая принадлежит плоскости этой грани и проходит через точку В1. Следовательно, 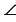 D1B1B = 900. По теореме Пифагора для
D1B1B = 900. По теореме Пифагора для 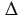 D1B1B запишем: BD12 = В1В2 + В1D12 . ABCDA1B1C1D1 - прямоугольный параллелепипед, то есть основание A1B1C1D1 является прямоугольником, значит, В1D1 есть диагональ прямоугольника и В1D12 = В1С12 + В1А12. Следовательно, BD12 = В1В2 + В1С12 + В1А12, что и требовалось доказать.
D1B1B запишем: BD12 = В1В2 + В1D12 . ABCDA1B1C1D1 - прямоугольный параллелепипед, то есть основание A1B1C1D1 является прямоугольником, значит, В1D1 есть диагональ прямоугольника и В1D12 = В1С12 + В1А12. Следовательно, BD12 = В1В2 + В1С12 + В1А12, что и требовалось доказать.
Мы знаем, что площадь прямоугольника равна произведению его измерений. По аналогии для прямоугольного параллелепипеда справедливо:
| Объём прямоугольного параллелепипеда равен произведению трёх его измерений. |
Чтобы доказать данное утверждение воспользуемся принципом Кавальери:
Рассмотрим сначала прямоугольный параллелепипед с измерениями 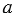 ,
, 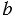 и 1 и куб с ребром 1, которые "стоят" на плоскости
и 1 и куб с ребром 1, которые "стоят" на плоскости 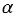 .
.
Нам известно, что данный куб будет являться единицей измерения объёмов, т.е. его объём равен 1. Любая секущая плоскость, параллельная плоскости 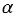 , даёт в качестве сечения данного параллелепипеда прямоугольник, площадь которого равна
, даёт в качестве сечения данного параллелепипеда прямоугольник, площадь которого равна 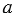
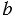 , а куба - квадрат, площадь которого равна 1. То есть площадь сечения параллелепипеда в
, а куба - квадрат, площадь которого равна 1. То есть площадь сечения параллелепипеда в 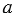
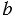 раз больше площади сечения куба, а, значит, согласно принципу Кавальери, объём рассматриваемого параллелепипеда больше объёма куба в
раз больше площади сечения куба, а, значит, согласно принципу Кавальери, объём рассматриваемого параллелепипеда больше объёма куба в 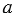
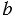 раз, то есть равен
раз, то есть равен 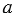
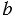 .
.
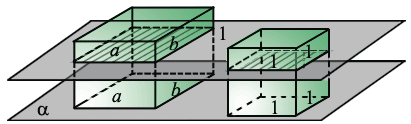
Далее рассмотрим два прямоугольных параллелепипеда с измерениями 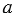 ,
, 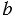 ,
, 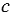 и
и 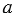 ,
, 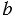 , 1, которые "стоят" на плоскости
, 1, которые "стоят" на плоскости 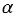 так, чтобы основания принадлежащие этой плоскости имели измерения
так, чтобы основания принадлежащие этой плоскости имели измерения 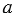 ,
, 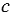 и
и 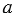 , 1.
, 1.
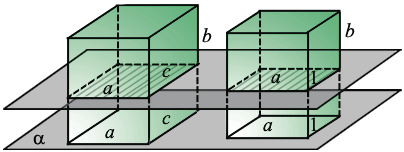
Объём второго параллелепипеда равен 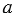
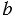 (см. доказано выше). Любая секущая плоскость, параллельная плоскости
(см. доказано выше). Любая секущая плоскость, параллельная плоскости 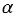 , даёт в качестве сечения первого параллелепипеда прямоугольник, площадь которого равна
, даёт в качестве сечения первого параллелепипеда прямоугольник, площадь которого равна 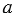
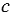 , а второго - прямоугольник, площадь которого равна
, а второго - прямоугольник, площадь которого равна 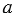 . То есть площадь сечения первого параллелепипеда в
. То есть площадь сечения первого параллелепипеда в 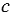 раз больше площади сечения второго параллелепипеда, а, значит, согласно принципу Кавальери, объём первого параллелепипеда больше объёма второго параллелепипеда в
раз больше площади сечения второго параллелепипеда, а, значит, согласно принципу Кавальери, объём первого параллелепипеда больше объёма второго параллелепипеда в 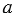
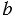 раз, то есть равен V =
раз, то есть равен V = 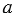
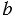
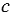 , что и требовалось доказать.
, что и требовалось доказать.
В прямоугольном параллелепипеде с измерениями 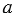 ,
, 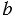 ,
, 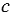 , который изображен выше, площадь основания S равна
, который изображен выше, площадь основания S равна 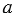
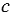 , а высота
, а высота 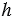 равна боковому ребру:
равна боковому ребру: 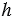 =
= 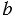 . Значит, формулу V =
. Значит, формулу V = 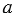
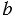
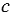 можно записать в виде: V = S
можно записать в виде: V = S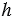 .
.
Объём прямоугольного параллелепипеда
| Объём прямоугольного параллелепипеда равен произведению площади основания на высоту. |
Объём призмы
| Объём призмы равен произведению площади основания на высоту. |
Советуем посмотреть:
Параллельность и перпендикулярность прямых и плоскостей в пространстве
Правило встречается в следующих упражнениях:
7 класс
Задание 1193, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1197, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1198, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1236, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1237, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1307, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник