Призма

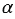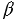Призму можно построить следующим образом. Рассмотрим параллельные плоскости   и . В плоскости 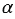возьмём произвольный многоугольник А₁А₂...A_n, а в плоскости  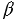- равный ему многоугольник В₁В₂...B_n, причём так, чтобы равные стороны А₁А₂ и В₁В₂, А₂А₃ и В₂В₃, ..., A_nA₁ и B_nB₁ этих многоугольников были параллельными сторонами  четырёхугольников А₁А₂В₂В₁, А₂А₃В₃В₂, ..., A_nA₁B₁B_n. 

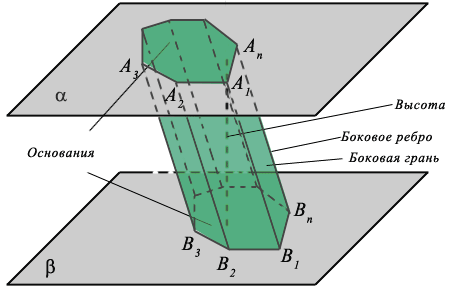
Указанные четырёхугольники являются параллелограммами, так как их противоположные стороны равны и параллельны по построению.

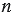- угольная призма - это многогранник А₁А₂А₃...A_nB₁B₂...B_n, который составлен из дух равных 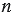- угольников А₁А₂...A_n и В₁В₂...B_n - оснований призмы и 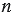параллелограммов А₁А₂В₂В₁, ..., А_nA₁B₁B_n - боковых граней призмы. Отрезки А₁В₁, ..., A_nB_n называются боковыми рёбрами призмы. Все они параллельны и равны друг другу.

Призма называется прямой, если все её боковые рёбра перпендикулярны к плоскостям её оснований.

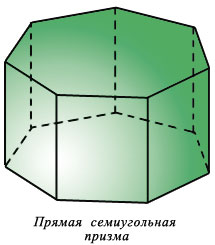
В ином случае призма называется наклонной.

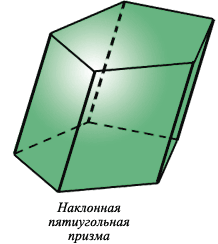
Правильная призма - это прямая призма, основаниями которой являются правильные многоугольники.

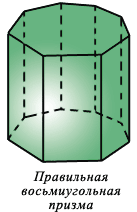
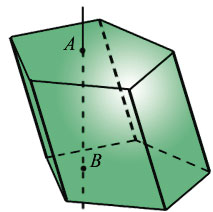
Все высоты призмы равны и параллельны друг другу. Для того чтобы построить высоту, необходимо выбрать произвольную точку А на одном из оснований и провести через неё прямую, которая будет перпендикулярна плоскости второго основании и пересечёт её в точке В. Тогда отрезок АВ и будет являться высотой призмы.