Связь между координатами вектора его начала и конца
Для того, чтобы определить координаты (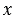 ,
, 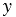 ) точки М в прямоугольной системе координат через точку М проводим прямые перпендикулярные к осям координат и обозначаем через М1 и М2 точки пересечения этих прямых с осями
) точки М в прямоугольной системе координат через точку М проводим прямые перпендикулярные к осям координат и обозначаем через М1 и М2 точки пересечения этих прямых с осями 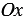 и
и 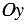 соответственно (Рис. 1).
соответственно (Рис. 1).
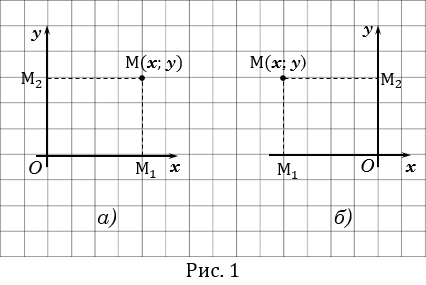
Число  (абсцисса точки М) определяется так:
(абсцисса точки М) определяется так:  = ОМ1, если М1 точка положительной полуоси (Рис. 1,
= ОМ1, если М1 точка положительной полуоси (Рис. 1,  ),
), 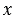 = - ОМ1, если М1 - точка отрицательной полуоси (Рис. 1, б);
= - ОМ1, если М1 - точка отрицательной полуоси (Рис. 1, б); 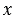 = 0, если М1 совпадает с точкой
= 0, если М1 совпадает с точкой 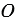 .
.
Аналогично определяется число 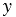 (ордината точки М). На рисунке 2 изображена прямоугольная система координат
(ордината точки М). На рисунке 2 изображена прямоугольная система координат 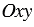 и отмечены точки:
и отмечены точки:
А(4; 3), В(- 5; 2), С(- 3,5;0).
На рисунке 3 вектор  называется радиус-вектором точки М.
называется радиус-вектором точки М.
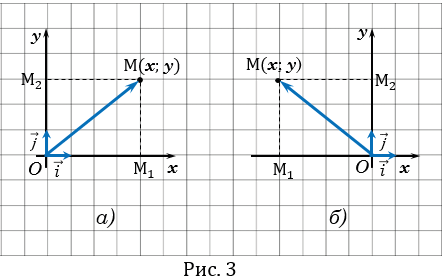
| Координаты точки М равны соответствующим координатам ее радиус-вектора. |
Доказательство
Дано: М(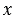 ,
, 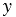 ),
), 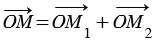 - радиус-вектор.
- радиус-вектор.
Доказать: 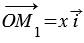 ,
, 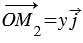 .
.
Доказательство:
Если 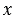
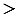 0 (как на рисунке 3,
0 (как на рисунке 3, 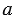 ), то
), то 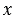 = ОМ1, а векторы
= ОМ1, а векторы 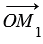 и
и 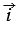 сонаправлены. Поэтому
сонаправлены. Поэтому 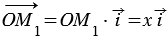 .
.
Если 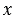
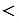 0 (как на рисунке 3, б), то
0 (как на рисунке 3, б), то 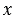 = - ОМ1, а векторы
= - ОМ1, а векторы 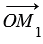 и
и 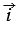 противоположно направлены. Поэтому
противоположно направлены. Поэтому 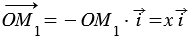 .
.
Если 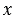 = 0, то
= 0, то 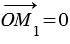 и равенство
и равенство 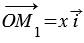 также будет справедливо.
также будет справедливо.
Получаем, что в любом случае 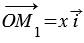 . Аналогично доказывается, что
. Аналогично доказывается, что 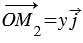 .
.
Следовательно, 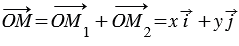 , значит, координаты радиус-вектора
, значит, координаты радиус-вектора 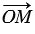 равны
равны 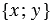 , т.е. равны соответствующим координатам точки М. Что и требовалось доказать.
, т.е. равны соответствующим координатам точки М. Что и требовалось доказать.
Рассмотрим вектор 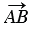 в прямоугольной системе координат
в прямоугольной системе координат 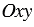 и выразим его координаты через координаты его начала А и конца В. Пусть точка А имеет координаты (
и выразим его координаты через координаты его начала А и конца В. Пусть точка А имеет координаты (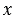 1,
1, 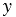 1), а точка В - координаты (
1), а точка В - координаты (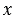 2,
2, 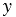 2) (Рис. 4).
2) (Рис. 4).
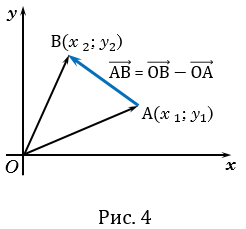
Вектор 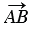 равен разности векторов
равен разности векторов 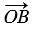 и
и 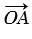 , значит, его координаты равны разностям соответствующих координат векторов
, значит, его координаты равны разностям соответствующих координат векторов 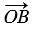 и
и 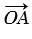 . Но
. Но 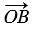 и
и 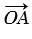 - радиус-векторы точек В и А, и поэтому
- радиус-векторы точек В и А, и поэтому 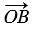 имеет координаты
имеет координаты  , а
, а 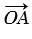 имеет координаты
имеет координаты 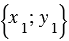 . Следовательно, вектор
. Следовательно, вектор 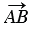 имеет координаты
имеет координаты 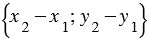 .
.
Вывод:
| Каждая координата вектора равна разности соответствующих координат его конца и начала. |
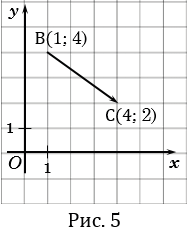
На рисунке 5 точки В и С имеют координаты (1; 4) и (4; 2), поэтому координаты вектора 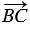 равны
равны 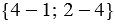 или
или 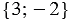 .
.
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Простейшие задачи в координатах
Взаимное расположение двух окружностей
Правило встречается в следующих упражнениях:
7 класс
Задание 935, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 939, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 946, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 947, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 949, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 991, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 992, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1006, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник