Простейшие задачи в координатах
Метод координат - это подход к изучению свойств геометрических фигур, используя методы алгебры.
Задачи
1. Координаты середины отрезка.
Дано: система координат 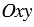 , А(
, А(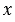 1;
1; 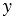 1), В(
1), В(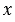 2;
2; 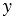 2), С середина отрезка АВ.
2), С середина отрезка АВ.
Выразить: координаты С(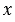 ;
; 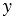 ) через координаты концов отрезка АВ.
) через координаты концов отрезка АВ.
Решение:
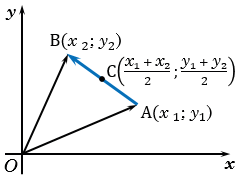
С - середина отрезка АВ, поэтому 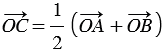 . (1)
. (1)
(Доказательство утверждения (1) приведено в разделе "Применение векторов к решению задач").
Координаты векторов 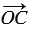 ,
, 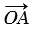 и
и 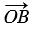 равны соответствующим координатам точек С, А и В:
равны соответствующим координатам точек С, А и В:
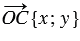 ,
, 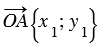 и
и 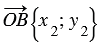 .
.
Записывая равенство (1) в координатах, получим:
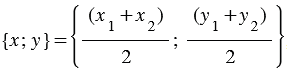 , следовательно,
, следовательно, 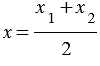 и
и 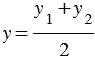 .
.
Вывод:
| Каждая координата середины отрезка равна полусумме соответствующих координат его концов. |
2. Вычисление длины вектора по его координатам.
Дано: 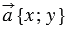 .
.
Доказать: 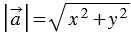 .
.
Доказательство:
1. 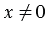 и
и 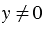 .
.
Отложим от начала координат вектор 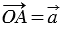 и проведем через точку А перпендикуляры АА1 и АА2 к осям
и проведем через точку А перпендикуляры АА1 и АА2 к осям 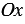 и
и 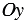 .
.
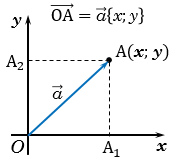
Координаты точки А равны координатам вектора 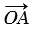 , т.е. (
, т.е. (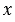 ;
; 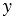 ). Поэтому
). Поэтому 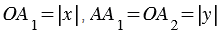 . По теореме Пифагора:
. По теореме Пифагора: 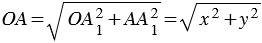 .
.
Но 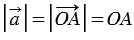 , следовательно,
, следовательно, 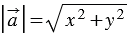 . Что и требовалось доказать.
. Что и требовалось доказать.
2. 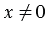 и
и 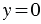 .
.
Отложим от начала координат вектор 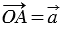 , учитывая то, что
, учитывая то, что 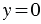 .
.
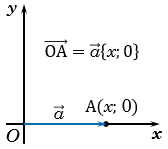
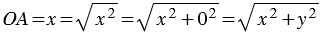 .
.
Но 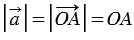 , следовательно,
, следовательно, 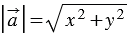 . Что и требовалось доказать.
. Что и требовалось доказать.
3. 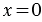 и
и 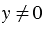 .
.
Отложим от начала координат вектор 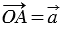 , учитывая то, что
, учитывая то, что 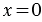 .
.
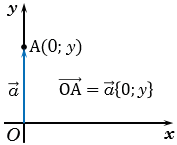
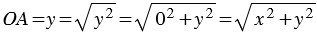 .
.
Но 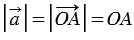 , следовательно,
, следовательно, 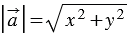 . Что и требовалось доказать.
. Что и требовалось доказать.
Вывод:
| Длина вектора равна квадратному корню из суммы квадратов координат данного вектора. |
3. Расстояние между двумя точками.
Дано: М1(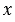 1;
1; 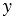 1), М2(
1), М2(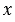 2;
2; 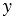 2),
2), 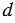 - расстояние между М1 и М2.
- расстояние между М1 и М2.
Выразить: 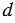 через координаты М1 и М2.
через координаты М1 и М2.
Решение:
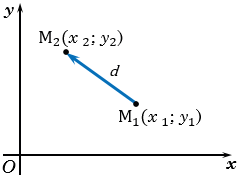
Рассмотрим вектор 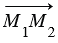 , каждая его координата равна разности соответствующих координат его конца и начала, т.е.
, каждая его координата равна разности соответствующих координат его конца и начала, т.е. 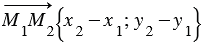 . Следовательно, длина этого вектора:
. Следовательно, длина этого вектора: 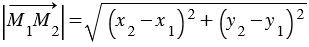 .
.
Но 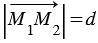 , значит, расстояние
, значит, расстояние 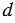 между точками М1(
между точками М1(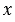 1;
1; 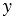 1) и М2(
1) и М2(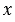 2;
2; 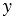 2) выражается формулой:
2) выражается формулой:
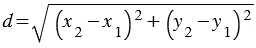 .
.
Вывод:
| Расстояние между двумя данными точками равно корню квадратному из суммы квадратов разностей соответствующих координат данных точек. |
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Взаимное расположение двух окружностей
Правило встречается в следующих упражнениях:
7 класс
Задание 936, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 938, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 939, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 946, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 951, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 956, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 997, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1009, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1073, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 283, Макарычев, Миндюк, Учебник