Задание 253 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник. Страница 75
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№253 учебника 2013-2022 (стр. 75):
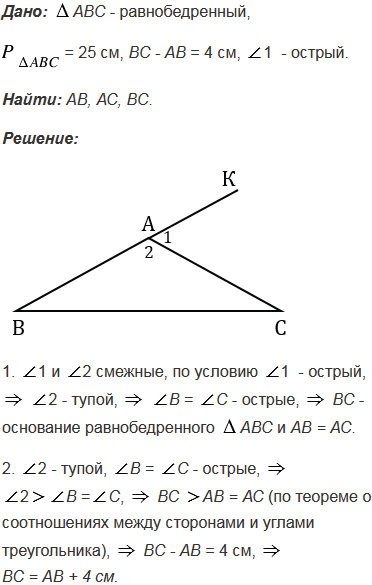
Периметр равнобедренного треугольника равен 25 см, разность двух сторон равна 4 см, а один из его внешних углов острый. Найдите стороны треугольника.
№253 учебника 2023-2024 (стр. 75):
Существует ли треугольник со сторонами: а) 1 м, 2 м и 3 м; б) 1,2 дм, 1 дм и 2,4 дм?
Подсказка
№253 учебника 2013-2022 (стр. 75):
Вспомните:
- Какой треугольник называется равнобедренным.
- Какой угол называется внешним.
- Что такое периметр треугольника.
- Какой угол называется острым, какой тупым.
- Теорему о соотношениях между сторонами и углами треугольника.
- Какие углы называются смежными и их свойство.
№253 учебника 2023-2024 (стр. 75):
Вспомните:
- Какая фигура называется треугольником.
- Неравенство треугольника.
Ответ
№253 учебника 2013-2022 (стр. 75):



№253 учебника 2023-2024 (стр. 75):
а) 1 м + 2 м = 3 м, что противоречит неравенству треугольника, 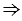 треугольник не существует.
треугольник не существует.
Ответ: не существует.
б) 1,2 дм + 1 дм = 2, 2 дм < 2,4 дм, что противоречит неравенству треугольника, 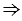 треугольник не существует.
треугольник не существует.
Ответ: не существует.
Пояснения:
Для того, чтобы ответить на вопрос существует ли треугольник с данными сторонами, необходимо проверить выполняется ли неравенство треугольника для этих сторон.
а) Если мы сложим стороны длиной 1 м и 2 м, то получим что их сумма равна 3 м, т.е. третьей стороне, а по неравенству треугольника, сумма двух сторон треугольника должна быть больше третьей стороны, следовательно, треугольник с такими сторонами не существует.
б) Если мы сложим стороны длиной 1,2 дм и 1 дм то получим что их сумма равна 2,2 дм, что меньше 2,4 дм, т.е. сумма двух сторон треугольника получилась меньше третьей стороны, а по неравенству треугольника, сумма двух сторон треугольника должна быть больше третьей стороны, следовательно, треугольник с такими сторонами не существует.
Вернуться к содержанию учебника