Теорема об односторонних углах
Теорема
| Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800. |
Дано: 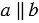 ,
, 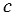 - секущая,
- секущая, 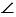 1 и
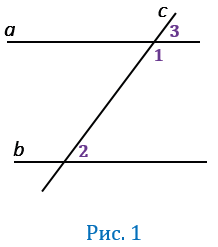
1 и 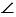 2 односторонние (Рис.1).
2 односторонние (Рис.1).
Доказать: 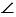 1 +
1 + 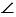 2 = 1800.
2 = 1800.
Доказательство:
По условию 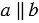 , значит соответственные углы 2 и 3 равны, т.е.
, значит соответственные углы 2 и 3 равны, т.е. 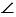 2 =
2 = 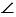 3 (по теореме о соответственных углах). При этом
3 (по теореме о соответственных углах). При этом 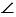 1 и
1 и 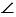 3 - смежные, следовательно, их сумма равна 1800, т.е.
3 - смежные, следовательно, их сумма равна 1800, т.е. 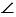 1 +
1 + 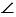 3 = 1800.
3 = 1800.
Из равенств 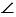 2 =
2 =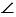 3 и
3 и 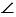 1 +
1 +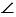 3 = 1800 следует, что
3 = 1800 следует, что 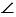 1 +
1 +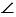 2 = 1800. Что и требовалось доказать.
2 = 1800. Что и требовалось доказать.
Советуем посмотреть:
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Правило встречается в следующих упражнениях:
7 класс
Задание 298, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 377, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 387, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 390, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 391, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 826, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 891, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1043, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1072, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник