Аксиомы геометрии

Аксиома - исходное положение о свойствах геометрических фигур, которое принимается без доказательства и на основе которого далее доказываются теоремы и вообще строится вся геометрия. Все аксиомы являются наглядно очевидными и не вызывают сомнений.

Геометрия, в которой сначала формулируются исходные положения - аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, называется евклидовой геометрией.

К аксиомам относятся следующие утверждения:

Аксиомы о взаимном расположении точек и прямой

1. Каждой прямой принадлежит по крайней мере две точки.
2. Имеются по крайней мере три точки, не лежащие на одной прямой.
3. Через любые две точки проходит прямая, и притом только одна.
4. Из трех точек прямой одна и только одна лежит между двумя другими.
5. Каждая точка О прямой разделяет ее на две части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
6. Каждая прямая 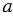разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой 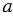, а любые две точки разных полуплоскостей лежат по разные стороны от прямой .

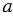Аксиомы о наложении и равенстве фигур

7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
8. На любом луче от его начала можно отложить отрезок, равный данному и притом только один.
9. От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.
10. Любой угол hk можно совместить наложением с равным ему углом h₁k₁ двумя способами: 1) так, что луч h совместится с лучом h₁, а луч k - с лучом k₁; 2) так, что луч h совместится с лучом k₁, а луч k - с лучом h₁.
11. Любая фигура равна самой себе.
12. Если фигура Ф равна фигуре Ф₁, то фигура Ф₁ равна фигуре Ф.
13. Если фигура Ф₁ равна фигуре Ф₂, а фигура Ф₂ равна фигуре Ф₃, то фигура Ф₁ равна фигуре Ф₃.

Аксиомы об измерении отрезков

14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
15. При выбранной единице измерения отрезков  для любого положительного числа существует отрезок, длина которого выражается этим числом.

Аксиома параллельности

16. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.