Теорема об углах с соответственно параллельными сторонами

Теорема

Дано: АОВ, А₁О₁В₁, ОА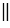О₁А₁, ОВ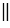О₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180⁰.

Доказательство:

Если угол АОВ - развернутый, значит лучи ОА  и ОВ будут лежать на одной прямой, при этом по условию ОА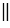О₁А₁, ОВ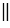О₁В₁, значит точки О₁А₁  и О₁В₁  также будут лежать на одной прямой, следовательно, А₁О₁В₁  - будет развернутым, тогда АОВ = А₁О₁В₁ (Рис. 1).

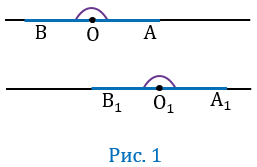
Если угол АОВ - неразвернутый, то возможны два случая расположения углов АОВ и А₁О₁В₁.

1 случай

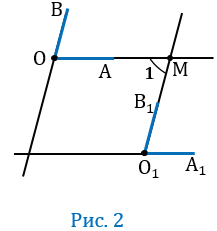
Прямая О₁В₁ пересекает прямую О₁А₁ и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М (смотри следствие 1⁰ из аксиомы параллельных прямых). Параллельные прямые ОВ и О₁В₁ пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О₁В₁ и ОА (Рис.2) равен углу АОВ, т.е. 1 = АОВ (по теореме о накрест лежащих углах). Параллельные прямые ОА и О₁А₁ пересечены секущей О₁М, поэтому 1 = А₁О₁В₁.

Из равенств 1 = АОВ и 1 = А₁О₁В₁ следует, что АОВ =А₁О₁В₁.

2 случай

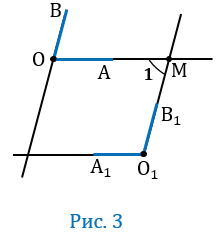
Прямая О₁В₁ пересекает прямую О₁А₁ и, следовательно, пересекает параллельную ей прямую ОА в некоторой точке М (смотри следствие 1⁰ из аксиомы параллельных прямых). Параллельные прямые ОВ и О₁В₁ пересечены секущей ОМ, поэтому один из углов (1), образованных при пересечении прямых О₁В₁ и ОА (Рис.3) равен углу АОВ, т.е. 1 +А₁О₁В₁ = 180⁰ (по теореме об односторонних углах). Параллельные прямые ОА и О₁А₁ пересечены секущей О₁М, поэтому 1 = А₁О₁В₁.

Из равенств 1 = АОВ и 1 +А₁О₁В₁ = 180⁰ следует, что АОВ +А₁О₁В₁ = 180⁰. Что и требовалось доказать.