Теорема об углах с соответственно перпендикулярными сторонами
Теорема
| Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 1800. |
Дано:  АОВ,
АОВ,  А1О1В1, ОА
А1О1В1, ОА О1А1, ОВ
О1А1, ОВ О1В1.
О1В1.
Доказать:  АОВ =
АОВ =  А1О1В1 или
А1О1В1 или  АОВ +
АОВ +  А1О1В1 = 1800.
А1О1В1 = 1800.
Доказательство:
1 случай
Пусть угол АОВ - развернутый (Рис. 1).
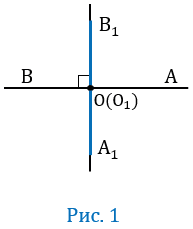
Угол АОВ - развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОА О1А1, ОВ
О1А1, ОВ О1В1, значит, лучи О1А1 и О1В1 также будут лежать на одной прямой, следовательно,
О1В1, значит, лучи О1А1 и О1В1 также будут лежать на одной прямой, следовательно,  А1О1В1 - будет развернутым, тогда
А1О1В1 - будет развернутым, тогда  АОВ =
АОВ =  А1О1В1.
А1О1В1.
2 случай
Пусть угол АОВ - прямой, т.е. равен 900 (Рис.2).
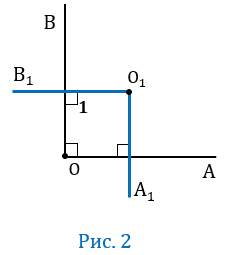
 АОВ = 900, то ОА
АОВ = 900, то ОА ОВ, при этом по условию ОА
ОВ, при этом по условию ОА О1А1, следовательно, ОВ
О1А1, следовательно, ОВ О1А1. Итак, О1В1 - секущая относительно прямых ОВ и О1А1, ОВ
О1А1. Итак, О1В1 - секущая относительно прямых ОВ и О1А1, ОВ О1А1, тогда по теореме об односторонних углах их сумма равна 1800, т.е.
О1А1, тогда по теореме об односторонних углах их сумма равна 1800, т.е.  1 +
1 +  А1О1В1 = 1800, откуда
А1О1В1 = 1800, откуда  А1О1В1 = 1800 -
А1О1В1 = 1800 - 1, при этом по условию ОВ
1, при этом по условию ОВ О1В1, значит
О1В1, значит  1 - прямой, т.е.
1 - прямой, т.е.  1 = 900, следовательно,
1 = 900, следовательно,  А1О1В1 = 1800 - 900 = 900. Из равенств
А1О1В1 = 1800 - 900 = 900. Из равенств  АОВ = 900 и
АОВ = 900 и  А1О1В1 = 900 следует, что
А1О1В1 = 900 следует, что  АОВ =
АОВ =  А1О1В1 и
А1О1В1 и  АОВ +
АОВ +  А1О1В1 = 900 + 900 = 1800.
А1О1В1 = 900 + 900 = 1800.
3 случай
Пусть О О1А1 (Рис.3).
О1А1 (Рис.3).
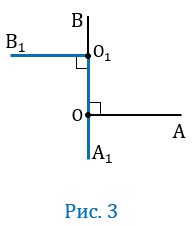
По условию О О1А1, тогда лучи ОВ и О1А1 будут лежать на одной прямой А1В. По условию ОА
О1А1, тогда лучи ОВ и О1А1 будут лежать на одной прямой А1В. По условию ОА О1А1, ОВ
О1А1, ОВ О1В1, значит, ОА и О1В1 будут перпендикулярны одной прямой А1В, следовательно, ОА
О1В1, значит, ОА и О1В1 будут перпендикулярны одной прямой А1В, следовательно, ОА О1В1. Итак, ОА
О1В1. Итак, ОА О1В1, А1В - секущая относительно прямых ОА и О1В1, тогда по теореме о накрест лежащих углах
О1В1, А1В - секущая относительно прямых ОА и О1В1, тогда по теореме о накрест лежащих углах  АОВ =
АОВ =  А1О1В1, причем, учитывая то, что ОА
А1О1В1, причем, учитывая то, что ОА О1А1, ОВ
О1А1, ОВ О1В1 эти углы будут прямые, т.е.
О1В1 эти углы будут прямые, т.е.  АОВ =
АОВ =  А1О1В1 = 900, тогда
А1О1В1 = 900, тогда  АОВ +
АОВ +  А1О1В1 = 900 + 900 = 1800.
А1О1В1 = 900 + 900 = 1800.
4 случай
Пусть О О1В1 (Рис.4).
О1В1 (Рис.4).
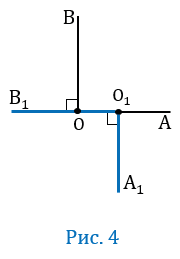
По условию О О1В1, тогда лучи ОА и О1В1 будут лежать на одной прямой В1А. По условию ОА
О1В1, тогда лучи ОА и О1В1 будут лежать на одной прямой В1А. По условию ОА О1А1, ОВ
О1А1, ОВ О1В1, значит ОВ и О1А1 будут перпендикулярны одной прямой В1А, следовательно, ОВ
О1В1, значит ОВ и О1А1 будут перпендикулярны одной прямой В1А, следовательно, ОВ О1А1. Итак, ОВ
О1А1. Итак, ОВ О1А1, В1А - секущая относительно прямых ОВ и О1А1, тогда по теореме о накрест лежащих углах
О1А1, В1А - секущая относительно прямых ОВ и О1А1, тогда по теореме о накрест лежащих углах  АОВ =
АОВ =  А1О1В1, причем, учитывая то, что ОА
А1О1В1, причем, учитывая то, что ОА О1А1, ОВ
О1А1, ОВ О1В1 эти углы будут прямые, т.е.
О1В1 эти углы будут прямые, т.е.  АОВ =
АОВ =  А1О1В1 = 900, тогда
А1О1В1 = 900, тогда  АОВ +
АОВ +  А1О1В1 = 900 + 900 = 1800.
А1О1В1 = 900 + 900 = 1800.
5 случай
Пусть угол АОВ - острый, т.е. меньше 900, при этом О О1А1, О
О1А1, О О1В1 (Рис.5).
О1В1 (Рис.5).
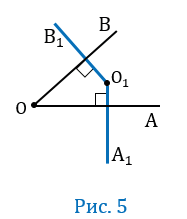
Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОА ОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВ
ОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВ ОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).
ОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).
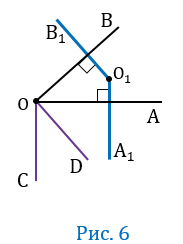
Получим, что  АОВ = 900 -
АОВ = 900 -  АОD, а
АОD, а  СОD = 900 -
СОD = 900 -  АОD, значит
АОD, значит  АОВ =
АОВ =  СОD. Стороны угла СОD соответственно параллельны сторонам угла А1О1В1, т.е. ОС
СОD. Стороны угла СОD соответственно параллельны сторонам угла А1О1В1, т.е. ОС О1А1 (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОА
О1А1 (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОА ОС и по условию ОА
ОС и по условию ОА О1А1), также ОD
О1А1), также ОD О1В1 (т.к. по построению ОВ
О1В1 (т.к. по построению ОВ ОD и по условию ОВ
ОD и по условию ОВ О1В1), поэтому по теореме об углах с соответственно параллельными сторонами либо
О1В1), поэтому по теореме об углах с соответственно параллельными сторонами либо  СОD =
СОD =  А1О1В1, либо
А1О1В1, либо  СОD +
СОD +  А1О1В1 = 1800. Следовательно, учитывая то, что
А1О1В1 = 1800. Следовательно, учитывая то, что  АОВ =
АОВ =  СОD получим, либо
СОD получим, либо  АОВ =
АОВ =  А1О1В1, либо
А1О1В1, либо  АОВ +
АОВ +  А1О1В1 = 1800.
А1О1В1 = 1800.
6 случай
Пусть угол АОВ - тупой, т.е. меньше 1800, но больше 900, при этом О О1А1, О
О1А1, О О1В1 (Рис.7).
О1В1 (Рис.7).
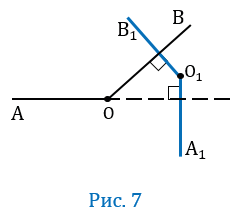
Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).
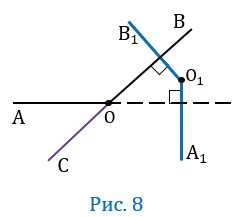
Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А1О1В1. Следовательно, либо  АОС +
АОС +  А1О1В1 = 1800, либо
А1О1В1 = 1800, либо  АОС =
АОС =  А1О1В1 (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 1800, значит
А1О1В1 (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 1800, значит  АОС = 1800 -
АОС = 1800 -  АОВ, следовательно, в первом случае 1800 -
АОВ, следовательно, в первом случае 1800 -  АОВ +
АОВ +  А1О1В1 = 1800, откуда
А1О1В1 = 1800, откуда  АОВ =
АОВ =  А1О1В1, а во втором случае 1800 -
А1О1В1, а во втором случае 1800 -  АОВ =
АОВ =  А1О1В1, откуда
А1О1В1, откуда  АОВ +
АОВ +  А1О1В1 = 1800. Что и требовалось доказать.
А1О1В1 = 1800. Что и требовалось доказать.
Советуем посмотреть:
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Правило встречается в следующих упражнениях:
7 класс
Задание 212, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1278, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник