Задание 341 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№341 учебника 2013-2022 (стр. 93):
В треугольнике АВС сторона АВ больше стороны АС, отрезок АD - биссектриса. Докажите, что 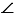 АDВ
АDВ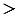
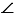 АDС и ВD
АDС и ВD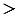 СD.
СD.
№341 учебника 2023-2024 (стр. 103):
Подсказка
№341 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Что такое биссектриса треугольника.
- Какие углы называются смежными и их свойство.
- Какой угол называется внешним углом треугольника.
- Первый признак равенства треугольников.
№341 учебника 2023-2024 (стр. 103):
Вспомните:
- Что называют окружностью, ее хорды.
- Что называют расстоянием от точки до прямой.
- Какой треугольник называют равнобедренным.
- Третий признак равенства треугольников.
Ответ
№341 учебника 2013-2022 (стр. 93):
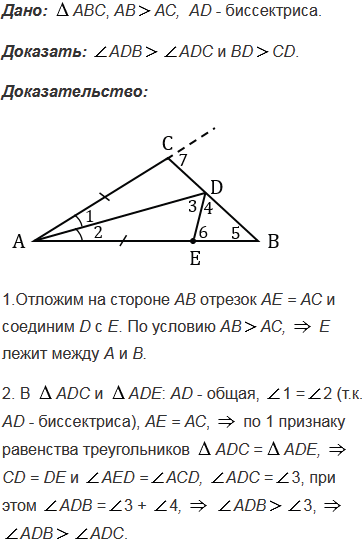



№341 учебника 2023-2024 (стр. 103):
Дано: окружность с центром О, АВ и СD - хорды, АВ = СD.
Доказать: что равные хорды окружности равноудалены от её центра.
Доказательство:
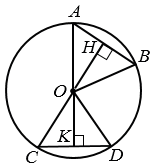
1. Проведем ОН 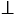 АВ и ОК
АВ и ОК 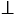 СD и докажем, что ОН = ОК.
СD и докажем, что ОН = ОК.
2. В 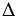 АОВ и
АОВ и 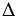 СОD:
СОD:
ОВ = ОС = ОВ = ОD - радиусы, и
АВ = СD, 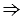
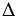 АОВ и
АОВ и 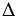 СОD - равнобедренные и
СОD - равнобедренные и 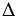 АОВ =
АОВ = 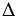 СОD (по 3 признаку равенства треугольников),
СОD (по 3 признаку равенства треугольников), 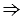 ОН = ОК (высоты равных равнобедренных треугольников).
ОН = ОК (высоты равных равнобедренных треугольников).
Пояснения:
Расстояние от точки до прямой - это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой. Поэтому для доказательства того, что равные хорды окружности равноудалены от её центра, из центра окружности О опускаем перпендикуляры ОН и ОК на хорды окружности АВ и СD и доказываем, что ОН = ОК.
В треугольниках АОВ и СОD:
ОВ = ОС = ОВ = ОD, так как эти отрезки являются радиусами окружности и АВ = СD, следовательно, треугольники АОВ и СОD - равнобедренные и 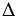 АОВ =
АОВ = 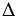 СОD по 3 признаку равенства треугольников (по трем сторонам). В равных равнобедренных треугольниках высоты проведенные к основаниям равны, поэтому ОН = ОК, т.к. по построению отрезки ОН и ОК высоты равных равнобедренных треугольников АОВ и СОD.
СОD по 3 признаку равенства треугольников (по трем сторонам). В равных равнобедренных треугольниках высоты проведенные к основаниям равны, поэтому ОН = ОК, т.к. по построению отрезки ОН и ОК высоты равных равнобедренных треугольников АОВ и СОD.
Вернуться к содержанию учебника