Упражнение 312 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 104

а) \((x^{2} - 4x - 12)^{2} + (x^{2} - 10x + 24)^{2} = 0\)

\( \begin{cases} (x^{2} - 4x - 12)^{2} = 0,\\ (x^{2} - 10x + 24)^{2} = 0 \end{cases} \)

\( \begin{cases} x^{2} - 4x - 12 = 0,\\ x^{2} - 10x + 24 = 0 \end{cases} \)

1) \(x^{2} - 4x - 12 = 0\)

\(D = (-4)^2 -4 \cdot1\cdot(-12)=\)

\(=16 + 48 = 64>0\) - 2 корня.

\(\sqrt {64} = 8\).

\( x_1 = \dfrac{4 + 8}{2\cdot1} = \dfrac{12}{2} = 6\).

\( x_2 = \dfrac{4 - 8}{2\cdot1} = \dfrac{-4}{2} = -2\).

2) \(x^{2} - 10x + 24 = 0\)

\(D = (-10)^2 - 4\cdot1\cdot24=\)

\(=100 - 96 = 4 > 0\) - 2 корня.

\(\sqrt 4 = 2\).

\( x_1 = \dfrac{10 + 2}{2\cdot1}=\dfrac{12}{2} = 6\).

\( x_2 = \dfrac{10 - 2}{2\cdot1}=\dfrac{8}{2} = 4\).

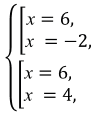
Ответ: \(x = 6.\)

б) \(|x^{2} + 15x + 50| + |x^{2} + 7x + 10| = 0\)

\( \begin{cases} |x^{2} + 15x + 50| = 0,\\ |x^{2} + 7x + 10| = 0 \end{cases} \)

\(\begin{cases} x^{2} + 15x + 50 = 0,\\ x^{2} + 7x + 10 = 0 \end{cases} \)

1) \(x^{2} + 15x + 50 = 0 \)

\(D = 15^2 - 4\cdot1\cdot50 =\)

\(=225 -200 = 25 > 0\) - 2 корня.

\(\sqrt {25} = 5\).

\(x_1 = \dfrac{-15 + 5}{2\cdot1} = \dfrac{-10}{2} = -5\).

\(x_2 = \dfrac{-15 - 5}{2\cdot1} = \dfrac{-20}{2} = -10\).

2) \(x^{2} + 7x + 10 = 0 \)

\(D = 7^2 - 4\cdot1\cdot10 = \)

\(= 49 - 40 = 9 > 0\) - 2 корня.

\(\sqrt 9 = 3\).

\(x_1 = \dfrac{-7 + 3}{2\cdot1} = \dfrac{-4}{2} = -2\).

\(x_2 = \dfrac{-7 - 3}{2\cdot1} = \dfrac{-10}{2} = -5\).

\((x + 5)(x + 2) = 0 \Rightarrow x = -5,\,-2.\)

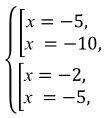
Ответ: \(x = -5.\)

Пояснения:

1. Сумма квадратов.

Квадрат любого действительного числа неотрицателен: \((A)^{2} \ge 0,\; (B)^{2} \ge 0.\) Поэтому \((A)^{2} + (B)^{2} = 0\) возможно только при \(A = 0\) и \(B = 0\). Отсюда в пункте а) получили систему двух квадратных уравнений и искали общий корень.

2. Сумма модулей.

Модуль числа тоже неотрицателен: \(|A| \ge 0\). Если \(|A| + |B| = 0\), то и \(|A| = 0\), и \(|B| = 0\), то есть \(A = 0\) и \(B = 0\). В пункте б) это привело к системе двух квадратных уравнений, общий корень которой и является решением исходного уравнения.