Упражнение 247 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 84

\(y = x^{2} - 3\) — это парабола, ветви которой направлены вверх, получается сдвигом параболы \(y = x^{2}\) вниз на 3 единицы.

\((0; -3)\) - вершина.

\(x = 0\) - ось симметрии.

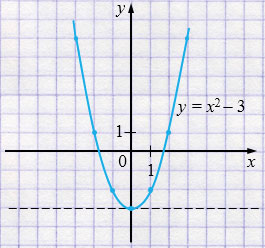
Нули функции:

\( x^{2} - 3 = 0\)

\( x^{2} = 3 \)

\(x = \pm \sqrt{3}\)

а) Функция принимает положительные значения, когда

\(x \in (-\infty; -\sqrt3) \cup (\sqrt3; +\infty)\).

б) Функция принимает отрицательные значения, когда \(x \in (-\sqrt3; \sqrt3)\).

Пояснения:

1. Парабола \(y = x^{2} - 3\) имеет вершину в точке \((0, -3)\). Это наименьшее значение функции. Коэффициент \(a = 1 >0\), поэтому ветви параболы направлены вверх.

2. Чтобы определить знак функции, необходимо найти точки, в которых она равна нулю, т.е. точки пересечения графика с осью абсцисс (нули функции).