Упражнение 176 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

\(\dfrac{4x}{x+2} = x - 3\)

\(\dfrac{4x + 8 - 8}{x+2}=\dfrac{4(x + 2) - 8}{x+2}=\)

\(=4 - \dfrac{8}{x+2}.\)

\(4 - \dfrac{8}{x+2} = x - 3\)

\(y = 4 - \dfrac{8}{x+2}\) - гипербола с асимптотами \(x = -2\) и \(y = 4\).

\(y=x-3\) - прямая.

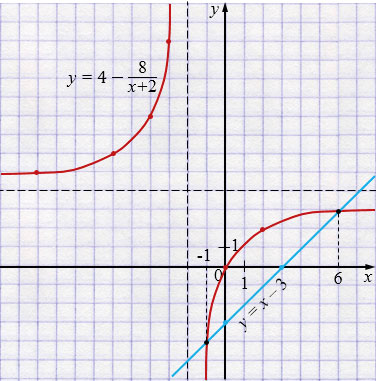
Ответ: \(x = -1\),  \(x = 6\).

Пояснения:

При графическом способе решения уравнений, нужно найти координаты точек пересечения графиков, которые соответствуют функциям, стоящим в левой и правой частях уравнения, так как абсциссы (координаты \(x\)) точек пересечения являются корнями исходного уравнения.

В рассматриваемом случае необходимо построить:

— прямую \(y=x-3\). Прямая однозначно задается двумя точками, поэтому составляем таблицу для двух значений \(x\) и по точкам полученным в таблице, чертим искомую прямую.

— гиперболу \(y=\dfrac{4x}{x+2}\).

Чтобы построить график гиперболы \(y=\dfrac{4x}{x+2}\), приводим эту функцию к виду \(\displaystyle y = \frac{k}{x - m} + n\). Для этого нужно выделить целую часть из дроби, соответствующей этой функции. При этом учитываем то, что значение выражения не изменится, если к нему прибавить и вычесть одно и то же число, а также помним:

\(\dfrac{ka + b}{a} = \dfrac{ka}{a} + \dfrac{b}{a} = k + \dfrac{b}{a}\).

Для функции вида \(\displaystyle y = \frac{k}{x - m} + n\) вертикальная асимптота: \(x = m\); горизонтальная асимптота: \(y = n.\) Асимптота - это прямая, к которой график функции неограниченно приближается, но никогда не пересекает.

\(y = 4 - \dfrac{8}{x+2}\) - графиком является гипербола, у которой вертикальная асимптота \(x=-2\), горизонтальная асимптота \(y=4\). Поэтому график — гипербола \(y=-\dfrac{8}{x}\), сдвинутая влево на \(2\) единицы и вверх на \(4\) единицы. Для построения графика функции пунктиром проводим асимптоты: прямую \(x = -2\) и прямую \(y = 4\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < -2\), другую для \(x > -2\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.

По построению видим, что прямая \(y=x-3\) пересекает гиперболу \(y = 4 - \dfrac{8}{x+2}\) в двух точках, которые имеют абсциссы \(x=-1\) и \(x=6\), являющиеся корнями исходного уравнения.

а) \(\sqrt[3]{10} \approx 2{,}15\)

б) \(\sqrt[3]{-38}= -\sqrt[3]{38} \approx -3{,}36\)

в) \(\sqrt[6]{18} \approx 1{,}62\)

г) \(\sqrt[4]{60} \approx 2{,}78\)

Пояснения:

В задаче требуется найти приближённые значения корней с точностью до сотых (до 0,01).

Программа вычисления корня \(n\)-й степени из положительного числа \(a\) выглядит так:

Например, чтобы найти \(\sqrt[3]{10}\), надо выполнить такую последовательность действий:

Важно: при округлении смотрим на следующую цифру — если она 5 или больше, увеличиваем предыдущую на 1.