Упражнение 172 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

\(y=\dfrac{3x-2}{x-2}\)

\(\dfrac{3x-2}{x-2} = \dfrac{3x-6 + 6 - 2}{x-2} =\)

\(=\dfrac{3(x-2) + 4}{x-2} = 3 + \dfrac{4}{x-2}. \)

\(y=3 + \dfrac{4}{x-2}\) - гипербола.

Асимптоты: \(x = 2\) и \(y = 3\).

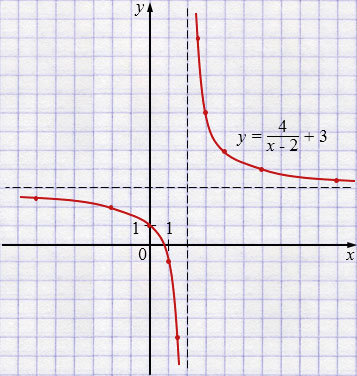
Нули функции: \(x \approx 0,7\).

Промежутки знакопостоянства:

\( y>0 \text{ при }\)

\(x\in(-\infty; 0,7) \cup (2;+\infty), \)

\[ y<0 \text{ при } x\in(0,7; 2). \]

Пояснения:

Чтобы построить график рассматриваемой функции, приводим эту функцию к виду \(\displaystyle y = \frac{k}{x - m} + n\). Для этого нужно выделить целую часть из дроби, соответствующей этой функции. При этом учитываем то, что значение выражения не изменится, если к нему прибавить и вычесть одно и то же число, а также помним:

\(\dfrac{ka + b}{a} = \dfrac{ka}{a} + \dfrac{b}{a} = k + \dfrac{b}{a}\).

Для функции вида \(\displaystyle y = \frac{k}{x - m} + n\) вертикальная асимптота: \(x = m\); горизонтальная асимптота: \(y = n.\) Асимптота - это прямая, к которой график функции неограниченно приближается, но никогда не пересекает.

\(y=3 + \dfrac{4}{x-2}\) - графиком является гипербола, у которой вертикальная асимптота \(x=2\), горизонтальная асимптота \(y=3\). Поэтому график — гипербола \(y=\dfrac{4}{x}\), сдвинутая вправо на \(2\) единицы и вверх на \(3\) единицы. Для построения графика функции пунктиром проводим асимптоты: прямую \(x = 2\) и прямую \(y = 3\). Так как гипербола состоит из двух ветвей, составляем две таблицы: одну для \(x < 2\), другую для \(x > 2\). Отметив точки в координатной плоскости, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы.

Нули функции - значения аргумента, при которых функция обращается в нуль (нули функции определяют точки пересечения с осью \(x\)). В нашем случае график функции пересекает ось \(x\) в одной точке, значит, функция имеет один нуль функции: \(x \approx 0,7\).

Промежутки знакопостоянства - промежутки, на которых функция сохраняет знак (на промежутках, расположенных выше оси \(x\) функция принимает положительные значения, на промежутках, расположенных ниже оси \(x\) функция принимает отрицательные значения). В рассматриваемом случае график функции расположен выше оси \(x\) на двух промежутках, то есть

\( y>0 \text{ при }\)

\(x\in(-\infty; 0,7) \cup (2;+\infty). \)

А ниже оси \(x\) на одном промежутке, то есть

\[ y<0 \text{ при } x\in(0,7; 2). \]

а) \((\sqrt[4]{7})^4=7\)

б) \((\sqrt[7]{-3})^7=-3\)

в) \((2\sqrt[4]{3})^4=2^4\cdot(\sqrt[4]{3})^4=\)

\(=16\cdot 3=48\)

г) \((-3\sqrt[5]{2})^5=(-3)^5\cdot(\sqrt[5]{2})^5=\)

\(=-243\cdot 2=-486\)

д) \((-\sqrt[7]{-28})^7= (-1)^7\cdot (\sqrt[7]{-28})^7= \)

\(=-1\cdot(-28) = 28\)

е) \((3\sqrt[3]{8})^3 = 3^3\cdot(\sqrt[3]{8})^3 =3\cdot8=24 \).

Пояснения:

Основное правило:

\[ (\sqrt[n]{a})^n=a \]

То есть корень и степень одинакового порядка взаимно уничтожают друг друга.

Также используется свойство степени:

\[ (ab)^n=a^n b^n \]

И правило степени отрицательного числа:

\[ (-a)^n = \begin{cases} a^n, & \text{если } n \text{ чётное} \\ -a^n, & \text{если } n \text{ нечётное} \end{cases} \]