Упражнение 171 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 66

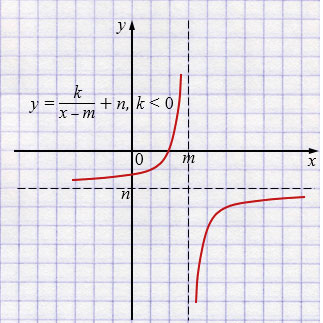
а) \(y=\dfrac{k}{x-m}+n\), где \(k<0\), если:

\(m>0,\; n<0\).

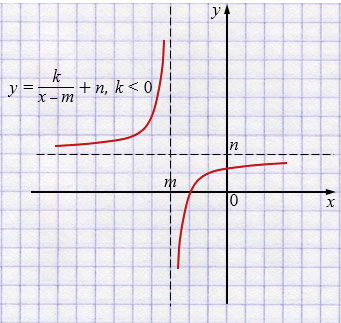
б) \(y=\dfrac{k}{x-m}+n\), где \(k<0\), если:

\(m<0,\; n>0\).

Пояснения:

1. Основные правила:

— Функция вида \(\displaystyle y=\frac{k}{x-m}+n\) представляет собой гиперболу.

— Вертикальная асимптота определяется знаменателем: \[x=m.\]

— Горизонтальная асимптота: \[y=n.\]

Асимптота - это прямая, к которой график функции неограниченно приближается, но никогда не пересекает.

— Расположение ветвей определяется знаком числителя \(k\):

\(\,\,\,\bullet\) при \(k>0\) — ветви в I и III четвертях;

\(\,\,\,\bullet\) при \(k<0\) — во II и IV четвертях.

а) Вертикальная асимптота: \(x=m\), а так как \(m>0\), она расположена справа от оси \(y\).

Горизонтальная асимптота: \(y=n\), и поскольку \(n<0\), она проходит ниже оси \(x\).

Поскольку \(k<0\), ветви гиперболы находятся во II и IV четвертях относительно своих асимптот.

б) Вертикальная асимптота: \(x=m\), где \(m<0\) — расположена слева от оси \(y\).

Горизонтальная асимптота: \(y=n\), где \(n>0\) — выше оси \(x\).

При \(k<0\) ветви гиперболы также будут расположены во II и IV четвертях относительно асимптот.