Упражнение 1132 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1132 учебника 2023-2025 (стр. 254):
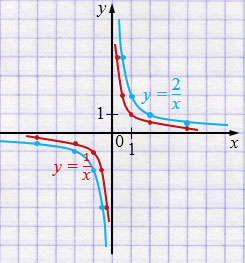
Изобразите схематически в одной системе координат графики функций \( y = \dfrac{1}{x} \) и \( y = \dfrac{2}{x} \). Имеют ли эти графики общие точки? Обоснуйте свой ответ алгебраически.
№1132 учебника 2013-2022 (стр. 256):
Расстояние между пристанями \(A\) и \(B\) теплоход проходит по течению за 5 ч, а против течения — за 6 ч. За сколько часов проплывает по течению это расстояние плот?
Подсказка
№1132 учебника 2023-2025 (стр. 254):
Вспомните:
- График функции обратной пропорциональности (\(y = \frac{k}{x}\)).
- Числовые промежутки.
- Координаты точки.
- Дробные рациональные уравнения.
- Линейное уравнение с одной переменной.
- Рациональные дроби.
- Подобные слагаемые.
№1132 учебника 2013-2022 (стр. 256):
Вспомните:
- Задачи на движение.
- Решение задач с помощью систем уравнений.
- Способ подстановки при решении систем уравнений.
- Уравнения с двумя переменными, их свойства.
- Умножение обыкновенных дробей.
- Подобные слагаемые.
- Вычитание дробей с разными знаменателями.
- Деление и дроби.
- Деление обыкновенных дробей.
- Сокращение дробей.
Ответ
№1132 учебника 2023-2025 (стр. 254):
\( y = \dfrac{1}{x} \) и \( y = \dfrac{2}{x} \)
\(D(y) =(-\infty; 0) \cup (0; +\infty)\).
\( \dfrac{1}{x} = \dfrac{2}{x} \), \(x \neq 0\)
\(x =2x \)
\(2x - x = 0\)
\(x = 0\) - не подходит, значит, графики не имеют общих точек.
Ответ: общих точек нет.
Пояснения:
Обе функции являются функциями обратной пропорциональности \(y = \frac{k}{x}\) и имеют одинаковый вид графика — гиперболу. При \(k> 0\) график функции \(y = \frac{k}{x}\) расположен в 1 и 3 координатных четвертях. Число \(k\) также определяет, насколько график «растянут» от осей координат.
— У функции \( y = \dfrac{1}{x} \) график расположен ближе к осям координат.
— У функции \( y = \dfrac{2}{x} \) график расположен дальше от осей координат.
Графики функций \( y = \dfrac{1}{x} \) и \( y = \dfrac{2}{x} \) не имеют общих точек.
Чтобы обосновать то, что графики не имеют общих точек, алгебраически, нужно приравнять рассматриваемые функции и решить уравнение относительно \(x\). При решении уравнения получили, что \(x = 0\), но это не подходит по области допустимых значений, в знаменателе не может стоять \(0\), так как на ноль делить нельзя. Значит, уравнение не имеет корней, а это говорит о том, что графики рассматриваемых функций не пересекаются.
№1132 учебника 2013-2022 (стр. 256):
Пусть \(x\) км/ч — собственная скорость теплохода, \(y\) км/ч — скорость течения, \(S\) км — расстояние между пристанями.
1) Составим систему уравнений:
\( \begin{cases} \frac{S}{x+y} = 5, /\times(x + y) \\ \frac{S}{x-y} = 6 /\times(x - y) \end{cases} \)
\( \begin{cases} S=5(x+y), / : 5 \\ S = 6(x - y) / : 6\end{cases} \)
\( \begin{cases} \frac{S}{5} = x + y, \\ \frac{S}{6} = x-y \end{cases} \) \((+)\)
\( \begin{cases} \frac{S}{5} + \frac{S}{6} = 2x, /\times 30 \\ \frac{S}{6} = x-y \end{cases} \)
\( \begin{cases} 6S + 5S = 60x, \\ \frac{S}{6} = x-y \end{cases} \)
\( \begin{cases} 11S = 60x, \\ \frac{S}{6} = x-y \end{cases} \)
\( \begin{cases} x=\frac{11S}{60}, \\ \frac{S}{6} = \frac{11}{60}S-y \end{cases} \)
\( \begin{cases} x=\frac{11S}{60}, \\ y = \frac{11S}{60}-\frac{S}{6}^{\color{blue}{\backslash10}} \end{cases} \)
\( \begin{cases} x=\frac{11S}{60}, \\ y = \frac{11S}{60}-\frac{10S}{60} \end{cases} \)
\( \begin{cases} x=\frac{11S}{60}, \\ y = \frac{S}{60} \end{cases} \)
2) \(\frac Sy = \frac{S}{\frac {S}{60}} = \cancel S\cdot \frac {60}{\cancel S} =60 \) (ч)
Ответ: плот проплывает расстояние за \(60\) ч.
Пояснения:
Решаем задачу с помощью системы уравнений.
Вводим обозначения:
\(x\) км/ч — собственная скорость теплохода, \(y\) км/ч — скорость течения, \(S\) км — расстояние между пристанями.
При движении по течению скорость увеличивается на скорость течения (\(x+y\)), а против течения — уменьшается (\(x-y\)).
Чтобы найти время, нужно расстояние разделить на скорость, тогда можем составить систему уравнений:
\( \begin{cases} \frac{S}{x+y} = 5, \\ \frac{S}{x-y} = 6 .\end{cases} \)
Решаем систему относительно переменных \(x\) и \(y\) способом подстановки. Из первого уравнения выражаем переменную \(x\), подставляем полученное выражение во второе уравнение и выражаем переменную \(y\).
Скорость плота равна скорости течения реки, то есть \(\frac{S}{60}\) км/ч. Значит, время, за которое плот преодолеет расстояние \(S\) равно:
\(\frac Sy = \frac{S}{\frac {S}{60}} = \cancel S\cdot \frac {60}{\cancel S} =60 \) (ч).
Вернуться к содержанию учебника