Упражнение 890 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

\(7{,}5 \leq a \leq 7{,}6\) и \(5{,}4 \leq b \leq 5{,}5\)

\(S = a \cdot b.\)

\(7{,}5\cdot5,4 \leq ab \leq 7{,}6\cdot5,5\)

\(40,5 \leq S \leq 41,8\)

Ответ: помещение подойдет для библиотеки.

Пояснения:

Площадь прямоугольника равна произведение его длины и ширины.

Если \(a\) и \(b\) - стороны прямоугольника, то его площадь:

\(S = ab\).

Чтобы понять подойдет ли данное помещение под библиотеку, оцениваем его площадь, учитывая то, что:

если почленно перемножить верные неравенства одного знака, левые и правые части которых - положительные числа, то получится верное неравенство.

Получили, что наименьшее значение площади данного помещения 40,5 м², наибольшее значение площади 41,8 м². Для библиотеки требуется комната площадью не менее 40 м², значит, рассматриваемое помещение подойдет для библиотеки.

а) \( \begin{cases} \dfrac{x}{3}+\dfrac{x}{4}<7,  /\times 12 \\[2pt] 1-\dfrac{x}{6}>0   /\times 6 \end{cases} \)

\( \begin{cases} 4x+3x < 84, \\ 6 - x > 0   /\times 6 \end{cases} \)

\( \begin{cases} 7x < 84, / :7 \\ -x > -6  / : (-1) \end{cases} \)

\( \begin{cases} x < 12, \\ x < 6 \end{cases} \)

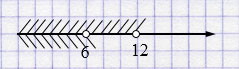
Ответ: \((-\infty; 6)\)

б) \( \begin{cases} y-\dfrac{y-1}{2}>1, /\times 2 \\[2pt] \dfrac{y}{3} < 5  /\times3 \end{cases} \)

\( \begin{cases} 2y-(y-1) > 2,\\[2pt] y < 15 \end{cases} \)

\( \begin{cases} 2y-y+1 > 2,\\[2pt] y < 15 \end{cases} \)

\( \begin{cases} y > 2 - 1,\\[2pt] y < 15 \end{cases} \)

\( \begin{cases} y > 1,\\[2pt] y < 15 \end{cases} \)

Ответ: \((1; 15)\)

в) \( \begin{cases} \dfrac{3x-1}{2}-x\le 2, /\times 2 \\[2pt] 2x-\dfrac{x}{3}\ge 1  /\times 3 \end{cases} \)

\( \begin{cases}3x-1-2x\le 4, \\[2pt] 6x-x\ge 3 \end{cases} \)

\( \begin{cases}x-1\le 4, \\[2pt] 5x\ge 3  / : 5 \end{cases} \)

\( \begin{cases}x\le 4 + 1, \\[2pt] x\ge \frac35 \end{cases} \)

\( \begin{cases}x\le 5, \\[2pt] x\ge 0,6 \end{cases} \)

Ответ: \([0,6; 5].\)

г) \( \begin{cases} 2p-\dfrac{p-2}{5} > 4, /\times 5 \\[2pt] \dfrac{p}{2}-\dfrac{p}{8}\le 6 /\times 8 \end{cases} \)

\( \begin{cases} 10p-(p-2) > 20, \\[2pt] 4p -p\le 48 \end{cases} \)

\( \begin{cases} 10p-p+2 > 20, \\[2pt] 3p\le 48 \end{cases} \)

\( \begin{cases} 9p > 20 - 2, \\[2pt] 3p\le 48 \end{cases} \)

\( \begin{cases} 9p > 18,  / : 9 \\[2pt] 3p\le 48  / : 3 \end{cases} \)

\( \begin{cases} p > 2, \\[2pt] p \le 16 \end{cases} \)

Ответ: \((2; 16].\)

Пояснения:

Чтобы решить систему неравенств, нужно найти пересечение решений неравенств системы, то есть найти множество чисел, которое является одновременно решением и одного неравенства и решением другого неравенства. Если решения неравенств не пересекаются, то система решений не имеет.

При решении неравенств системы используем то, что:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.

- если обе части неравенства разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

Если знак неравенства нестрогий (\(\geq\)  или \(\leq\)), то точку на координатной прямой делаем закрашенной, а при записи промежутка используем квадратную скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

Приведение дробей к общему знаменателю:

\(\dfrac{A}{m}\pm\dfrac{B}{n}=\dfrac{An\pm Bm}{mn}\).

Раскрытие скобок:

\(-(a - b) = b - a\).