Упражнение 355 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№355 учебника 2023-2025 (стр. 84):
Решите графически уравнение:
а) \(\sqrt{x} = 6 - x\);
б) \(\sqrt{x} = \frac{4}{x}\);
в) \(-x - 5 = \sqrt{x}\).
№355 учебника 2013-2022 (стр. 86):
Пользуясь графиком функции \(y = \sqrt{x}\), найдите:
а) значение \(\sqrt{x}\) при \(x = 2{,}5;\;5{,}5;\;8{,}4\);
б) значение \(x\), которому соответствует \(\sqrt{x} = 1{,}2;\;1{,}7;\;2{,}5\).
Подсказка
№355 учебника 2023-2025 (стр. 84):
Вспомните:
- Функцию квадратного корня (\(y=\sqrt x\)) и ее график.
- Линейную функцию, ее график.
- Функцию обратной пропорциональности, ее график.
- Координаты точки.
- Что называют арифметическим квадратным корнем.
- Деление и дроби.
- Деление рациональных чисел.
- Деление десятичных дробей.
№355 учебника 2013-2022 (стр. 86):
Вспомните:
- Функцию \(y=\sqrt x\) и ее график.
- Координаты точки.
- Перпендикулярные прямые.
- Параллельные прямые.
Ответ
№355 учебника 2023-2025 (стр. 84):
а) \(\sqrt{x} = 6 - x\)
\(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
\(y = 6 - x\)
| \(x\) | 0 | 6 |
| \(y\) | 6 | 0 |

Ответ: \(x = 4\).
б) \(\sqrt{x} = \frac{4}{x}\)
\(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
\(y = \frac{4}{x}\)
| \(x\) | 8 | 4 | 2 | 1 | 0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 | 8 |
| \(x\) | -8 | -4 | -2 | -1 | -0,5 |
| \(y\) | -0,5 | -1 | -2 | -4 | -8 |
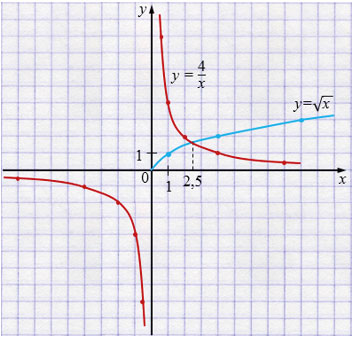
Ответ: \(x = 2,4\).
в) \(-x - 5 = \sqrt{x}\)
\(y = -x - 5\)
| \(x\) | 0 | -5 |
| \(y\) | -5 | 0 |
\(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
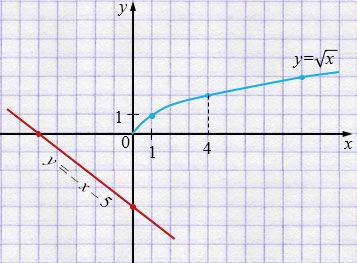
Ответ: решений нет.
Пояснения:
Чтобы решить уравнение графически, строим два графика функции относительно левой и правой части уравнения, абсциссы (координаты \(x\)) точек пересечения этих графиков и являются решениями уравнения. Если графики не пересекаются, то уравнение решений не имеет.
Область определения функции
\(y=\sqrt{x}\) задаётся условием \(x\ge0\). Строится график по точкам для неотрицательных значений \(x\).
Функция вида \(y = kx+b\) является линейной, ее графиком является прямая. Строим прямую по двум точкам.
Функция \(y=\frac{k}{x}\) - функция обратной пропорциональности, графиком является гипербола (две ветви). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\)).
№355 учебника 2013-2022 (стр. 86):
а) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
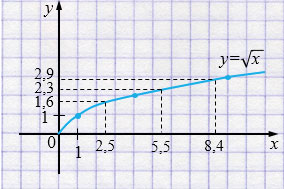
Если \(x = 2{,}5\), то \(\sqrt{x} =1,6 \).
Если \(x=5{,}5\), то \(\sqrt{x} =2,3 \).
Если \(x = 8{,}4\), то \(\sqrt{x} =2,9 \).
б) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
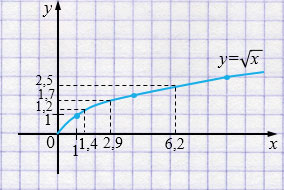
Если \(\sqrt{x} = 1{,}2\), то \(x = 1,4\).
Если \(\sqrt{x} = 1{,}7\), то \(x = 2,9\).
Если \(\sqrt{x} = 2{,}5\), то \(x = 6,2\).
Пояснения:
Использованные правила и приёмы:
Функция \(y=\sqrt{x}\) определена при \(x\ge0\). Строим график функции по точкам.
а) Чтобы найти значения \(\sqrt{x}\) которые соответствуют заданным значениям \(x\) по графику функции \(y=\sqrt{x}\), через заданные значения к оси \(x\) проводим перпендикулярные прямые, эти прямые пересекут график в некоторые точках, через эти точки чертим прямые параллельные оси \(x\), которые пересекут ось \(y\) в значениях, соответствующих искомым значениям \(\sqrt{x}\).
б) Чтобы найти значения \(x\), которые соответствуют заданным значениям \(\sqrt{x}\) по графику функции \(y=\sqrt{x}\), через заданные значения к оси \(y\) проводим перпендикулярные прямые, эти прямые пересекут график в некоторые точках, через эти точки чертим прямые перпендикулярные к оси \(x\), которые пересекут ось \(x\) в значениях, соответствующих искомым значениям \(x\).
Вернуться к содержанию учебника