Упражнение 360 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№360 учебника 2023-2025 (стр. 85):
Имеет ли смысл выражение:
а) \(\sqrt{(-9)^2}\);
б) \(\bigl(\sqrt{-9}\bigr)^2\);
в) \(-\sqrt{9}^2\);
г) \(-\sqrt{(-9)^2}\)?
№360 учебника 2013-2022 (стр. 87):
(Для работы в парах.) Имеют ли общие точки графики функций:
а) \(y = \sqrt{x}\) и \(y = x\);
б) \(y = \sqrt{x}\) и \(y = 1000\);
в) \(y = \sqrt{x}\) и \(y = x + 10\);
г) \(y = \sqrt{x}\) и \(y = -x + 1{,}5\)?
При положительном ответе укажите координаты этих точек.
1) Распределите, кто выполняет задания а) и в), а кто - задания б) и г), и выполните их.
2) Проверьте друг у друга, верно ли выполнены задания. Исправьте замеченные ошибки.
3) Приведите примеры линейных функций, графики которых: не пересекают график функции \(y=\sqrt x\); пересекают его в одной точке; пересекают его в двух точках. Обсудите правильность этих примеров.
Подсказка
№360 учебника 2023-2025 (стр. 85):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Сравнение рациональных чисел.
№360 учебника 2013-2022 (стр. 87):
Вспомните:
- Функцию квадратного корня (\(y=\sqrt x\)) и ее график.
- Линейную функцию.
- Координаты точки.
- Что называют арифметическим квадратным корнем.
- Свойства уравнений.
- Вынесение общего множителя за скобки.
- Свойства умножения.
Ответ
№360 учебника 2023-2025 (стр. 85):
а) \(\sqrt{(-9)^2} = \sqrt{81} = 9\) - имеет смысл.
б) \((\sqrt{-9})^2\) - не имеет смысла,
так как \(-9 < 0\).
в) \(-\sqrt{9}^2 = -\bigl(\sqrt{9^2}\bigr) = -\sqrt{81} = -9\) - имеет смысл.
г) \(-\sqrt{(-9)^2} = -\sqrt{81} = -9\) - имеет смысл.
Пояснения:
Использованные правила:
1) Область определения корня: \(\sqrt{a}\) определён только если \(a \ge 0\).
2) Порядок вычислений: при \(\sqrt{(-9)^2}\) сначала возводят \(-9\) в квадрат, получают 81, затем извлекают корень.
3) В выражении \(\bigl(\sqrt{-9}\bigr)^2\) корень берётся от отрицательного числа — недопустимо.
4) В выражениях с внешним знаком «−» можно вычислять корень и степень внутри, а затем применять знак «−» снаружи.
№360 учебника 2013-2022 (стр. 87):
а) \(y = \sqrt{x}\) и \(y = x\)
\(\sqrt{x}=x\)
\( x = x^2\)
\( x - x^2 = 0\)
\( x(x-1)=0 \)
\(x=0\) или \(x - 1 = 0\)
\(x = 1\)
Если \(x = 0\), то \(y =0\).
Если \(x = 1\), то \(y =1\).
\((0,0)\) и \((1,1)\) - точки пересечения графиков функций \(y = \sqrt{x}\) и \(y = x\).
Ответ: графики пересекаются в двух точках \((0,0)\) и \((1,1)\).
б) \(y = \sqrt{x}\) и \(y = 1000\)
\(\sqrt{x}=1000\)
\( x = 1000^2 =\)
\(x = 1 000 000 \)
\(\bigl(1 000 000,\;1000\bigr)\) - точка пересечения графиков функций \(y = \sqrt{x}\) и \(y = 1000\).
Ответ: графики пересекаются в одной точке \(\bigl(1 000 000,\;1000\bigr)\).
в) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
\(y = x + 10\)
| \(x\) | 0 | -5 |
| \(y\) | 10 | 5 |
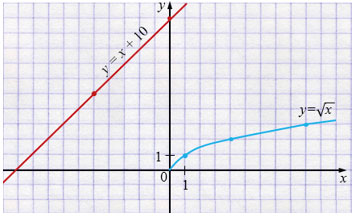
Ответ: графики не пересекаются.
г) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
\(y = -x + 1{,}5\)
| \(x\) | 0 | 3 |
| \(y\) | 1,5 | -1,5 |
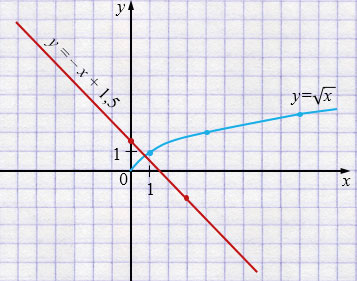
\((0,7; 0,8)\) - точка пересечения графиков \(y = \sqrt{x}\) и \(y = -x + 1{,}5\).
Ответ: графики пересекаются в одной точке \((0,7; 0,8)\).
Пояснения:
Использованные правила и приёмы:
1) Область определения функции
\(y=\sqrt{x}\) задаётся условием \(x\ge0\).
2) Для определения точек пересечения графиков в пунктах а) и б) приравниваем правые части данных функций и решаем уравнения, тем самым определяя координаты \(x\) точек пересечения рассматриваемых графиков, затем подставляя значение \(x\) в уравнение любой из этих функций находим координату \(y\) точки пересечения графиков.
3) Для определения точек пересечения графиков в пунктах в) и г) строим графики данных функций.
Вернуться к содержанию учебника