Упражнение 348 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 83
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№348 учебника 2023-2025 (стр. 83):
Пользуясь графиком функции \(y = \sqrt{x}\), найдите:
а) значение \(\sqrt{x}\) при \(x = 2{,}5;\;5{,}5;\;8{,}4\);
б) значение \(x\), которому соответствует \(\sqrt{x} = 1{,}2;\;1{,}7;\;2{,}5\).
№348 учебника 2013-2022 (стр. 83):
Решите уравнение и найдите с помощью калькулятора приближенные значения его корней (ответ округлите до сотых):
а) \(x^2 = 30\);
б) \(7x^2 = 10\);
в) \((x-3)^2 = 8\);
г) \((x + 1)^2 = 8\).
Подсказка
№348 учебника 2023-2025 (стр. 83):
Вспомните:
- Функцию \(y=\sqrt x\) и ее график.
- Координаты точки.
- Перпендикулярные прямые.
- Параллельные прямые.
№348 учебника 2013-2022 (стр. 83):
Вспомните:
- Что называют арифметическим квадратным корнем.
- Свойства уравнений.
- Деление и дроби.
- Деление десятичных дробей.
- Степень с натуральным показателем.
- Неправильные дроби.
- Смешанные числа.
- Сравнение рациональных чисел.
Ответ
№348 учебника 2023-2025 (стр. 83):
а) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
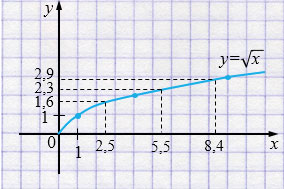
Если \(x = 2{,}5\), то \(\sqrt{x} =1,6 \).
Если \(x=5{,}5\), то \(\sqrt{x} =2,3 \).
Если \(x = 8{,}4\), то \(\sqrt{x} =2,9 \).
б) \(y = \sqrt{x}\)
| \(x\) | 0 | 1 | 4 | 9 |
| \(y\) | 0 | 1 | 2 | 3 |
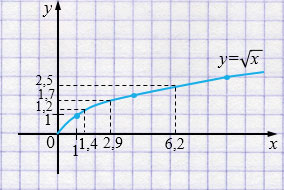
Если \(\sqrt{x} = 1{,}2\), то \(x = 1,4\).
Если \(\sqrt{x} = 1{,}7\), то \(x = 2,9\).
Если \(\sqrt{x} = 2{,}5\), то \(x = 6,2\).
Пояснения:
Использованные правила и приёмы:
Функция \(y=\sqrt{x}\) определена при \(x\ge0\). Строим график функции по точкам.
а) Чтобы найти значения \(\sqrt{x}\) которые соответствуют заданным значениям \(x\) по графику функции \(y=\sqrt{x}\), через заданные значения к оси \(x\) проводим перпендикулярные прямые, эти прямые пересекут график в некоторые точках, через эти точки чертим прямые параллельные оси \(x\), которые пересекут ось \(y\) в значениях, соответствующих искомым значениям \(\sqrt{x}\).
б) Чтобы найти значения \(x\), которые соответствуют заданным значениям \(\sqrt{x}\) по графику функции \(y=\sqrt{x}\), через заданные значения к оси \(y\) проводим перпендикулярные прямые, эти прямые пересекут график в некоторые точках, через эти точки чертим прямые перпендикулярные к оси \(x\), которые пересекут ось \(x\) в значениях, соответствующих искомым значениям \(x\).
№348 учебника 2013-2022 (стр. 83):
а) \(x^2 = 30 \)
\(x_1 = -\sqrt{30} \approx -5,48 \)
\(x_2 = \sqrt{30} \approx 5,48\).
Ответ: \(\pm5,48\).
б) \(7x^2 = 10\)
\(x^2 = \dfrac{10}{7} \)
\(x^2 = 1\dfrac{3}{7} \)
\(x_1 = -\sqrt{1\dfrac{3}{7}} \approx -1,20\)
\(x_2 = \sqrt{1\dfrac{3}{7}} \approx 1,20\)
Ответ: \(\pm1,20\).
в) \((x-3)^2 = 8\)
1) \(x - 3 = -\sqrt12\)
\(x - 3 = -3,46\)
\(x = -3,46 + 3\)
\(x = -0,46\)
2) \(x - 3 = \sqrt12\)
\(x - 3 = 3,46\)
\(x = 3,46 + 3\)
\(x = 6,46\)
Ответ: \( -0,46\) и \(6,46\).
г) \((x + 1)^2 = 8\)
1) \(x + 1 = -\sqrt8\)
\(x + 1 = -2,83\)
\(x = -2,83 -1\)
\(x = -3,83\)
2) \(x + 1 = \sqrt8\)
\(x + 1 = 2,83\)
\(x = 2,83 -1\)
\(x = 1,83\)
Ответ: \(-3,83\) и \(1,83\).
Пояснения:
Использованные правила:
1) Для уравнения вида \(ax^2=b\) (где \(a\neq0\)) получаем
\(x^2=\frac{b}{a}\) откуда:
\(x_1=-\sqrt{\frac{b}{a}}\) и \(x_2=\sqrt{\frac{b}{a}}\).
2) Так же учитываем то, что корни уравнения не изменяются при переносе слагаемых из одной части уравнения в другую со сменой знака на противоположный.
Вернуться к содержанию учебника