Упражнение 1026 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(ac+\dfrac{b}{c}\ge 2\sqrt{ab}\)

\( \frac{ac+\frac{b}{c}}{2}\ge\sqrt{ac\cdot\frac{b}{c}}\)

\( \frac{ac+\frac{b}{c}}{2}\ge\sqrt{ab} \)     \(/\times2\)

\(ac+\frac{b}{c}\ge 2\sqrt{ab}. \)

Что и требовалось доказать.

б) \(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge 8.\)

1) \(\frac{1+\dfrac{a^{2}}{bc}}{2} \ge \sqrt{1\cdot \frac{a^2}{bc}}\)      \(/\times2\)

\(1+\dfrac{a^{2}}{bc}  \ge 2\sqrt{ \frac{a^2}{bc}}\)

2) \(\frac{1+\dfrac{b^{2}}{ac}}{2} \ge \sqrt{1\cdot \frac{b^2}{ac}}\)      \(/\times2\)

\(1+\dfrac{b^{2}}{ac}  \ge 2\sqrt{ \frac{b^2}{ac}}\)

3) \(\frac{1+\dfrac{c^{2}}{ab}}{2} \ge \sqrt{1\cdot \frac{c^2}{ab}}\)      \(/\times2\)

\(1+\dfrac{c^{2}}{ab}  \ge 2\sqrt{\frac{c^2}{ab}}\)

4) Перемножаем неравенства:

\(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge2\sqrt{ \frac{a^2}{bc}}\cdot 2\sqrt{ \frac{b^2}{ac}} \cdot 2\sqrt{\frac{c^2}{ab}}\)

\(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge8\sqrt{ \frac{a^2b^2c^2}{bc\cdot ac \cdot ab}}\)

\(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge8\sqrt{ \frac{a^2b^2c^2}{a^2b^2c^2}}\)

\(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge8\sqrt{1}\)

\(\left(1+\dfrac{a^{2}}{bc}\right)\!\left(1+\dfrac{b^{2}}{ac}\right)\!\left(1+\dfrac{c^{2}}{ab}\right)\ge8\)

Что и требовалось доказать.

Пояснения:

При доказательстве используем соотношение между средним арифметическим и средним геометрическим двух положительных чисел: среднее арифметическое любых двух положительных чисел всегда больше или равно их среднему геометрическому.

Среднее арифметическое двух чисел равно сумме этих чисел, делённой на 2.

Среднее геометрическое двух чисел равно корню квадратному из произведения этих чисел.

Также при доказательстве используем то, что:

- если почленно перемножить верные неравенства одного знака, левые и правые части которых - положительные числа, то получится верное неравенство;

- если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство.

Свойство арифметического корня:

\(\sqrt a \cdot \sqrt b = \sqrt{ab}\).

\(\dfrac{4 - 3x}{2} - x < 11\)    \(/\times2\)

\(4 - 3x - 2x < 22\)

\(4 - 5x < 22\)

\(-5x <22-4\)

\(-5x < 18\)   \(/ : (-5)\)

\(x > -\frac{18}{5}\)

\(x > -3,6\)

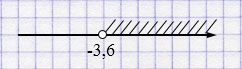
\(x \in (-3,6; +\infty)\)

Ответ: \(x = -3, -2, -1.\)

Пояснения:

При решении рассматриваемых неравенств помним:

- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;

- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Если знак неравенства строгий (\(>\)  или \(<\)), то точку на координатной прямой делаем "выколотой" (незакрашенной), при записи промежутка используем круглую скобку.

У \(-\infty\) и \(+\infty\) при записи промежутка скобка всегда круглая.

Так как требуется найти только целые отрицательные значения, то из промежутка \(x \in (-3,6; +\infty)\) это числа \(-3, -2, -1.\)