Упражнение 190 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№190 учебника 2023-2025 (стр. 49):
Решите графически уравнение:
а) \(\displaystyle \frac{8}{x} = x^2\);
б) \(\displaystyle \frac{8}{x} = x^3\).
№190 учебника 2013-2022 (стр. 47):
Задайте формулой обратную пропорциональность, зная, что её график проходит через точку:
а) \(A(8;\,0{,}125)\);
б) \(B\bigl(\frac{2}{3};\,1\frac{4}{5}\bigr)\);
в) \(C(-25;\,-0{,}2)\).
Подсказка
№190 учебника 2023-2025 (стр. 49):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Деление и дроби.
- Деление рациональных чисел.
- Умножение рациональных чисел.
- График квадратичной функции (парабола).
- График кубической параболы.
- Степень с натуральным показателем.
№190 учебника 2013-2022 (стр. 47):
Вспомните:
Ответ
№190 учебника 2023-2025 (стр. 49):
а) \(\displaystyle \frac{8}{x} = x^2\)
\(y= \frac{8}{x}\)
| \(x\) | -8 | -4 | -2 | -1 |
| \(y\) | -1 | -2 | -4 | -8 |
| \(x\) | 8 | 4 | 2 | 1 |
| \(y\) | 1 | 2 | 4 | 8 |
\(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |

Ответ: \(x = 2\).
б) \(\displaystyle \frac{8}{x} = x^3\)
\(y= \frac{8}{x}\)
| \(x\) | -8 | -4 | -2 | -1 |
| \(y\) | -1 | -2 | -4 | -8 |
| \(x\) | 8 | 4 | 2 | 1 |
| \(y\) | 1 | 2 | 4 | 8 |
\(y = x^3\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
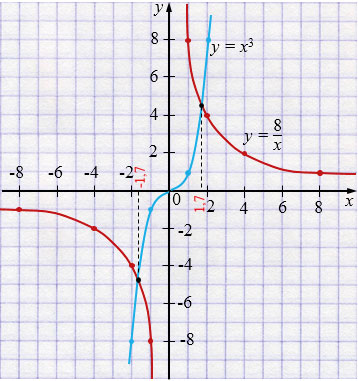
Ответ: \(x = -1,7\) и \(x = 1,7\).
Пояснения:
а) Чтобы решить графически уравнение \(\displaystyle \frac{8}{x} = x^2\), нужно найти точки пересечения двух графиков:
\(y=\frac{6}{x}\) и \(y = x^2\), где
\(y= \frac{8}{x}\) - функция обратной пропорциональности, графиком является гипербола (две ветви, расположенные в I и III координатных четвертях, так как \(k=8\)). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y = x^2\) - квадратичная функция, графиком которой является парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
б) Чтобы решить графически уравнение \(\displaystyle \frac{8}{x} = x^3\), нужно найти точки пересечения двух графиков:
\(y=\frac{6}{x}\) и \(y = x^3\), где
\(y= \frac{8}{x}\) - функция обратной пропорциональности, графиком является гипербола (две ветви, расположенные в I и III координатных четвертях, так как \(k=8\)). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y = x^3\) - кубическая функция, графиком которой является кубическая парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
№190 учебника 2013-2022 (стр. 47):
\( y = \frac{k}{x}, \)
а) \(A(8;\,0{,}125)\);
\( 0,125 = \frac{k}{8} \) /\(\times8\)
\(k = 1\)
Ответ: \( y = \frac{1}{x}.\)
б) \(B\bigl(\frac{2}{3};\,1\frac{4}{5}\bigr)\)
\( 1\frac{4}{5} = \frac{k}{\frac23} \) /\(\times\frac23\)
\(k= 1\frac{4}{5} \cdot\frac23\)
\(k= \frac{^3\cancel9}{5} \cdot\frac{2}{\cancel{3}}\)
\(k = \frac65=1,2\)
Ответ: \(y = \frac{1,2}{x}\).
в) \(C(-25;\,-0{,}2)\).
\( -0,2 = \frac{k}{-25} \) /\(\times(-25)\)
\(k = -0,2\cdot(-25)\)
\(k = 5\)
Ответ: \(y = \frac{5}{x}\).
Пояснения:
Использованные правила и приёмы:
• Функция обратной пропорциональности задаётся формулой \(y=\dfrac{k}{x}\).
• Число \(k\) находим, подставляя координаты данной точки в функцию \(y=\dfrac{k}{x}\) вместо \(x\) и \(y\).
• После вычисления \(k\) записываем итоговое уравнение \(y=\frac{k}{x}\).
При решении уравнений, чтобы найти \(k\), обе части уравнения умножили на знаменатель дроби.
Вернуться к содержанию учебника