Упражнение 186 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№186 учебника 2023-2025 (стр. 49):
На рисунке 6 построен график функции, заданной формулой \(\displaystyle y=\frac{8}{x}\). Найдите по графику:
а) значение \(y\), соответствующее значению \(x\), равному \(2;\;4;\;-1;\;-4;\;-5\);
б) значение \(x\), которому соответствует значение \(y\), равное \(-4;\;-2;\;8\).
№186 учебника 2013-2022 (стр. 47):
Постройте график функции \(y=\dfrac{6}{x}\) и, используя его, решите уравнение:
а) \(\displaystyle \frac{6}{x}=x\);
б) \(\displaystyle \frac{6}{x}=-x+6.\)
Подсказка
№186 учебника 2023-2025 (стр. 49):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Перпендикулярные прямые.
- Параллельные прямые.
№186 учебника 2013-2022 (стр. 47):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Деление и дроби.
- Деление рациональных чисел.
- График линейной функции.
Ответ
№186 учебника 2023-2025 (стр. 49):
а) Если \(x=2\), то \( y=4\).
Если \(x=4\), то \(y=2\).
Если \(x=-1\), то \(y=-8\).
Если \(x=-4\), то \(y=-2\).
Если \(x=-5\), то \(y=-1,6. \)
б) Если \(y = -4\), то \(x=-2\).
Если \(y=-2\),то \(x=-4\).
Если \(y=8\), то \(x=1. \)
Пояснения:
а) Чтобы определить по графику значения \(y\) при заданных значениях переменных \(x\), нужно через заданные значения \(x\) провести прямые перпендикулярные к оси \(x\) до пересечения с графиком и через точку на графике провести прямую, параллельную оси \(x\), которая пересечет ось \(y\) в нужной нам точке.
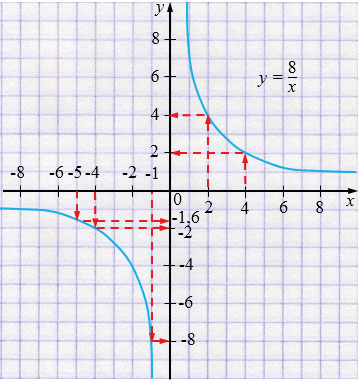
б) Чтобы определить по графику значения \(x\) при заданных значениях переменных \(y\), нужно через заданные значения \(y\) провести прямые параллельные оси \(x\) до пересечения с графиком и через точку на графике провести прямую, перпендикулярную оси \(x\), которая пересечет ось \(x\) в нужной нам точке.
№186 учебника 2013-2022 (стр. 47):
\(y=\frac{6}{x}\)
| \(x\) | -6 | -3 | -2 | -1 |
| \(y\) | -1 | -2 | -3 | -6 |
| \(x\) | 1 | 2 | 3 | 6 |
| \(y\) | 6 | 3 | 2 | 1 |

а) \( \frac{6}{x}=x \)
\(y=\frac{6}{x}\)
\(y = x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
Ответ: \(x=-2,4\) и \(x=2,4\).
б) \( \frac{6}{x}=-x+6 \)
\(y=\frac{6}{x}\)
\(y=-x+6\)
| \(x\) | 0 | 6 |
| \(y\) | 6 | 0 |
Ответ: \(x = 1,3\) и \(x = 4,7\).
Пояснения:
• Графиком обратной пропорциональности \(y=\frac{k}{x}\) является гипербола (две ветви). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
• Знак \(k\) определяет положение ветвей в координатных четвертях:
– Если \(k>0\), то ветви гиперболы лежат в I и III координатных четвертях;
– Если \(k<0\), то ветви гиперболы лежат во II и IV координатных четвертях.
а) Чтобы решить уравнение \( \frac{6}{x}=x \), нужно найти точки пересечения двух графиков:
\(y=\frac{6}{x}\) и \(y = x\),
где \(y = x\) - линейная функция, графиком которой является прямая (строим по двум точкам).
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
б) Чтобы решить уравнение \( \frac{6}{x}=-x + 6 \), нужно найти точки пересечения двух графиков:
\(y=\frac{6}{x}\) и \(y = -x+6\),
где \(y = -x + 6\) - линейная функция, графиком которой является прямая (строим по двум точкам).
Решением уравнения являются значения координаты \(x\) для точек пересечения графиков.
Вернуться к содержанию учебника