Упражнение 1172 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 230
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1172 учебника 2023-2025 (стр. 230):
Постройте график уравнения:
а) \(y = |x|\);
б) \(y = -|x|\).
№1172 учебника 2013-2022 (стр. 230):
Решите систему уравнений:
а) \( \begin{cases} 8x + 5y = 20,\\ 1{,}6x + 2y = 0; \end{cases} \)
б) \( \begin{cases} \tfrac{1}{7}x - \tfrac{1}{13}y = 1,\\ 13x - 7y = 5; \end{cases} \)
в) \( \begin{cases} -1{,}8x + 2{,}4y = 1,\\ 3x - 4y = 5; \end{cases} \)
г) \( \begin{cases} \tfrac{2}{3}x - \tfrac{1}{8}y = \tfrac{1}{2},\\ -16x + 3y = 12. \end{cases} \)
Подсказка
№1172 учебника 2023-2025 (стр. 230):
Вспомните:
- График линейной функции.
- Модуль числа.
№1172 учебника 2013-2022 (стр. 230):
Вспомните:
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Уравнения с двумя переменными, их свойства.
- Линейное уравнение с одной переменной, его свойства.
- Деление и дроби.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Подобные слагаемые.
Ответ
№1172 учебника 2023-2025 (стр. 230):
а) \(y = |x|\)
Если \(x\ge0\), то \(y = x\).
| \(x\) | 0 | 3 |
| \(y\) | 0 | 3 |
Если \(x<0\), то \(y = -x\).
| \(x\) | 0 | -3 |
| \(y\) | 0 | 3 |

б) \(y = -|x|\)
Если \(x\ge0\), то \(y = -x\).
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
Если \(x<0\), то \(y = -(-x)= x\).
| \(x\) | 0 | -3 |
| \(y\) | 0 | -3 |
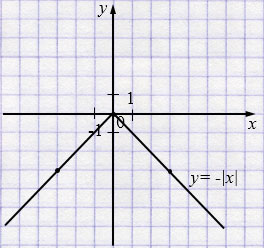
Пояснения:
– Функция задаётся по частям: \(|x|\) равен самому \(x\), если \(x\ge0\), и противоположному \(-x\), если \(x<0\).
– Каждый график представляет собой «угол» из двух лучей, являющихся биссектрисами координатных четвертей.
– В обеих функциях ключевая точка — вершина угла \((0;0)\).
№1172 учебника 2013-2022 (стр. 230):
а) \( \begin{cases} 8x + 5y = 20,\\ 1{,}6x + 2y = 0; /\times(-5) \end{cases} \)
\( \begin{cases} 8x + 5y = 20,\\ -8x - 10y = 0; \end{cases} \) \((+)\)
\( \begin{cases} -5y = 20,\\ -8x - 10y = 0; \end{cases} \)
\( \begin{cases} y = -\frac{20}{5},\\ 8x = -10y; \end{cases} \)
\( \begin{cases} y = -4,\\ 8x = -10\cdot(-4); \end{cases} \)
\( \begin{cases} y = -4,\\ 8x = 40; \end{cases} \)
\( \begin{cases} y = -4,\\ x = \frac{40}{8}; \end{cases} \)
\( \begin{cases} y = -4,\\ x = 5; \end{cases} \)
Ответ: \(x = 5\), \(y = -4\).
б) \( \begin{cases} \tfrac{1}{7}x - \tfrac{1}{13}y = 1, /\times(-91) \\ 13x - 7y = 5; \end{cases} \)
\( \begin{cases} -13x + 7y = -91,\\ 13x - 7y = 5; \end{cases} \) \((+)\)
\( \begin{cases} -0 = -86 - неверно,\\ 13x - 7y = 5; \end{cases} \)
Ответ: система не имеет решения.
в) \( \begin{cases} -1{,}8x + 2{,}4y = 1,\\ 3x - 4y = 5; /\times0,6 \end{cases} \)
\( \begin{cases} -1{,}8x + 2{,}4y = 1,\\ 1,8x - 2,4y = 3; \end{cases} \)
\( \begin{cases} 0 = 4 - неверно,\\ 1,8x - 2,4y = 3; \end{cases} \)
Ответ: система не имеет решения.
г) \( \begin{cases} \tfrac{2}{3}x - \tfrac{1}{8}y = \tfrac{1}{2}, /\times24 \\ -16x + 3y = 12. \end{cases} \)
\( \begin{cases} 16x - 3y = 12,\\ -16x + 3y = 12. \end{cases} \)
\( \begin{cases} 0 = 24 - неверно, \\ -16x + 3y = 12. \end{cases} \)
Ответ: система не имеет решения.
Пояснения:
Использованные приёмы:
1) Преобразование уравнений к целым коэффициентам умножением на общий знаменатель дробей, входящих в уравнение.
2) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
3) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
4) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
5) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
В пунктах б), в) и г) при сложении уравнений получается неверное числовое равенство, это говорит о том, что система не имеет решения.
Вернуться к содержанию учебника