Упражнение 1176 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 230
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1176 учебника 2023-2025 (стр. 230):
При каком значении \(b\) прямые
\( b x + 3y = 10 \) и \( x - 2y = 4 \)
пересекаются в точке, принадлежащей оси \(x\)?
№1176 учебника 2013-2022 (стр. 230):
(Для работы в парах.) Напишите уравнение вида \(y = kx + b\), график которого проходит через точки:
а) \(M(-1;1)\) и \(P(4;4)\);
б) \(A(-3;3)\) и \(B(3;-3)\).
1) Обсудите друг с другом ход решения задачи.
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Проверьте друг у друга, правильно ли составлены уравнения, построив соответствующие графики.
Подсказка
№1176 учебника 2023-2025 (стр. 230):
Вспомните:
- Что называют решением системы уравнений с двумя переменными.
- Уравнения с двумя переменными.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Деление десятичных дробей.
№1176 учебника 2013-2022 (стр. 230):
Вспомните:
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Уравнения с двумя переменными, их свойства.
- График линейной функции.
- Линейное уравнение с одной переменной, его свойства.
- Деление и дроби.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Подобные слагаемые.
- Деление десятичных дробей.
- Умножение десятичных дробей.
- Вычитание десятичных дробей.
Ответ
№1176 учебника 2023-2025 (стр. 230):
\( \begin{cases} b x + 3y = 10,\\ x - 2y = 4 \end{cases} \)
На оси \(x\): \(y = 0\)
\( \begin{cases} b x + 3\cdot0 = 10,\\ x - 2\cdot0 = 4 \end{cases} \)
\( \begin{cases} b x = 10,\\ x = 4 \end{cases} \)
\( \begin{cases} 4b = 10,\\ x = 4 \end{cases} \)
\( \begin{cases} b = \frac{10}{4},\\ x = 4 \end{cases} \)
\( \begin{cases} b = 2,5,\\ x = 4 \end{cases} \)
Ответ: при \(b = 2,5\).
Пояснения:
– Точка на оси \(x\) задаётся условием \(y=0\).
– Решение системы начинается с подстановки \(y=0\) в каждое уравнение, из второго уравнения тем самым находим \(x\).
– Затем найденное значение \(x\) подставляют в первое уравнение, чтобы определить \(b\).
№1176 учебника 2013-2022 (стр. 230):
а) \(M(-1;1)\) и \(P(4;4)\)
\(y = kx + b\)
\( \begin{cases} 1 = k\cdot(-1) + b,\\ 4 = k\cdot4 + b. \end{cases} \)
\( \begin{cases} 1 = -k + b, /\times(-1) \\ 4 = 4k + b. \end{cases} \)
\( \begin{cases} -1 = k - b, \\ 4 = 4k + b. \end{cases} \) \((+)\)
\( \begin{cases} 3 = 5k, \\ 4 = 4k + b. \end{cases} \)
\( \begin{cases} k = \frac35, \\ b = 4 - 4k \end{cases} \)
\( \begin{cases} k = 0,6, \\ b = 4 - 4\cdot0,6 \end{cases} \)
\( \begin{cases} k = 0,6, \\ b = 4 - 2,4 \end{cases} \)
\( \begin{cases} k = 0,6, \\ b = 1,6 \end{cases} \)
\(y = 0,6x + 1,6\)
| \(x\) | -1 | -6 |
| \(y\) | 1 | -2 |
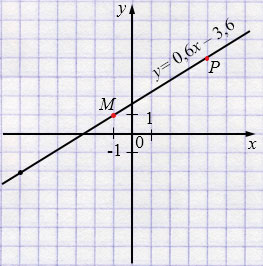
Ответ: \(y = 0,6x + 1,6\).
б) \(A(-3;3)\) и \(B(3;-3)\)
\(y = kx + b\)
\( \begin{cases} 3 = k\cdot(-3) + b,\\ -3 = k\cdot3 + b \end{cases} \)
\( \begin{cases} 3 = -3k + b,\\ -3 = 3k + b \end{cases} \) \((+)\)
\( \begin{cases} 0 = 2b,\\ -3 = 3k + b \end{cases} \)
\( \begin{cases} b = 0,\\ 3k = -b - 3 \end{cases} \)
\( \begin{cases} b = 0,\\ 3k = 0 - 3 \end{cases} \)
\( \begin{cases} b = 0,\\ 3k = -3 \end{cases} \)
\( \begin{cases} b = 0,\\ k = -1 \end{cases} \)
\(y = -x \)
| \(x\) | 1 | -4 |
| \(y\) | -1 | 4 |
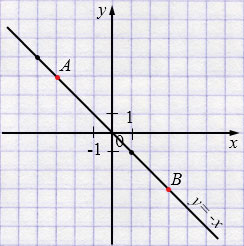
Ответ: \(y = -x. \)
Пояснения:
1) Линейная функция \(y=kx+b\) задаётся двумя параметрами \(k\) и \(b\).
2) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
3) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
4) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
5) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
6) Так находятся коэффициенты \(k\) и \(b\) определяется единственная прямая, проходящая через заданные точки.
7) Чтобы построить прямую достаточно две точки.
Вернуться к содержанию учебника