Упражнение 1151 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1151 учебника 2023-2025 (стр. 228):
Изобразите на координатной плоскости фигуру, которую задаёт система неравенств
\( \begin{cases} y \le -0,5x + 2,\\ x \ge 0,\\ y \ge 0, \end{cases} \)
и найдите её площадь.
№1151 учебника 2013-2022 (стр. 227):
Постройте график уравнения:
а) \(3(x - 2y) - 2(x - 4y) = 4\);
б) \(2(0{,}5x - 1{,}2y) - (0{,}6y + x) = 6\);
в) \(3(0{,}4y - 0{,}2x) - 4(0{,}3y - 0{,}6x) = 0{,}6\).
Подсказка
№1151 учебника 2023-2025 (стр. 228):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
- Умножение рациональных чисел.
- Прямоугольный треугольник.
- Как найти площадь прямоугольника.
- Умножение обыкновенных дробей.
№1151 учебника 2013-2022 (стр. 227):
Вспомните:
- Уравнение с двумя переменными, его график.
- Распределительное свойство умножения.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение десятичных дробей.
- Сложение и вычитание десятичных дробей.
- Подобные слагаемые.
- Деление десятичных дробей.
- Сокращение дробей.
Ответ
№1151 учебника 2023-2025 (стр. 228):
\( \begin{cases} y \le -0,5x + 2,\\ x \ge 0,\\ y \ge 0 \end{cases} \)
\(y = -0,5x + 2\)
| \(x\) | 0 | 4 |
| \(y\) | 2 | 0 |
\( \begin{cases} x \ge 0,\\ y \ge 0 \end{cases} \) - I координатная четверть.
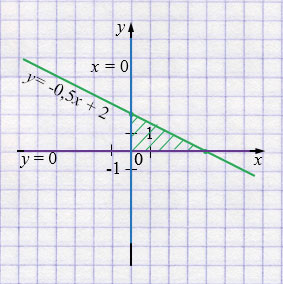
Область пересечения - прямоугольный треугольник.
\(S = \frac{1}{2}\cdot2 \cdot 4 = 4.\)
Ответ: площадь равна 4.
Пояснения:
Использованные правила и формулы:
– Пересечение полуплоскостей даёт геометрическую фигуру - прямоугольный треугольник.
– Площадь прямоугольника равна произведению его длины и ширины. Площадь прямоугольного треугольника равна половине площади прямоугольника, для которого катеты прямоугольного треугольника являются длиной и шириной. Значит, площадь прямоугольного треугольника равна половине произведения его катетов.
Подробности шагов:
Сначала выделили границы \(x\ge0\) и \(y\ge0\) — первая четверть координатной плоскости.
Затем прямая \(y=-0,5x+2\) ограничивает область сверху.
Решение системы неравенств - область пересечения - прямоугольный треугольник.
Катеты этого треугольника лежат вдоль осей \(Ox\) и \(Oy\) с длинами 4 и 2 соответственно.
Поэтому площадь равна половине произведения этих катетов.
№1151 учебника 2013-2022 (стр. 227):
а) \(3(x - 2y) - 2(x - 4y) = 4\)
\( 3x - 6y - 2x + 8y = 4\)
\(x + 2y = 4\)
\(2y = 4 - x \)
\(y = 2 - 0,5x \)
\(y = -0,5x+2 \)
| \(x\) | 0 | 4 |
| \(y\) | 2 | 0 |
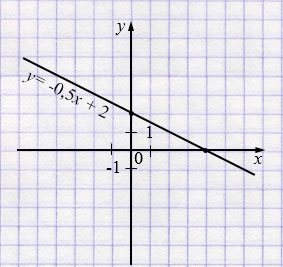
б) \(2(0{,}5x - 1{,}2y) - (0{,}6y + x) = 6\)
\( \cancel{x} - 2{,}4y - 0{,}6y - \cancel{x} = 6 \)
\( -3y = 6 \)
\(y = -\frac{6}{3}\)
\(y = -2\)
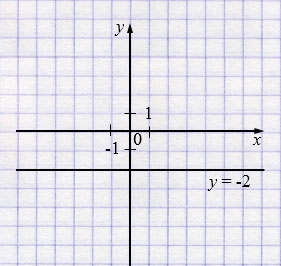
в) \(3(0{,}4y - 0{,}2x) - 4(0{,}3y - 0{,}6x) = 0{,}6\)
\(\cancel{1{,}2y} - 0{,}6x - \cancel{1{,}2y} + 2{,}4x = 0{,}6 \)
\( 1{,}8x = 0{,}6\)
\( x = \frac{0{,}6}{1{,}8} \)
\( x = \frac13 \)
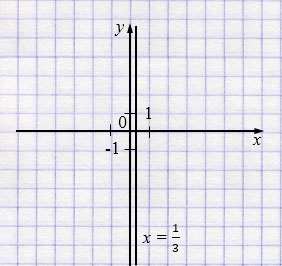
Пояснения:
– Любое уравнение вида \(ax + by = c\) задаёт на плоскости прямую.
– Чтобы построить прямую, удобно привести к виду \(y = kx + b\).
– Распределительное свойство умножения:
\(a(b + c) = ab + ac\).
– Приведение подобных членов:
\(ax + bx = (a + b)x\).
– Для прямой в виде \(y = -0,5x+2 \) достаточно отметить две точки и провести через них прямую.
– Горизонтальная прямая: \(y = -2\),
вертикальная прямая: \(x = \frac{1}{3}\).
Вернуться к содержанию учебника